题目内容
6.已知函数$f(x)=cos2xcosθ-sin2xcos({\frac{π}{2}-θ})({|θ|<\frac{π}{2}})$在$({-\frac{3π}{8},-\frac{π}{6}})$上单调递增,则$f({\frac{π}{16}})$的最大值为1.分析 利用三角函数恒等变换的应用化简可求f(x)=cos(2x+θ),由余弦函数的图象和性质可求θ的范围,进而即可得解.
解答 解:∵$f(x)=cos2xcosθ-sin2xcos({\frac{π}{2}-θ})({|θ|<\frac{π}{2}})$
=cos2xcosθ-sin2xsinθ
=cos(2x+θ),
又∵f(x)在$({-\frac{3π}{8},-\frac{π}{6}})$上单调递增,
∴2×(-$\frac{3π}{8}$)+θ≥2kπ+π,2×(-$\frac{π}{6}$)+θ≤2kπ+2π,k∈Z,
∵|θ|$<\frac{π}{2}$,解得:-$\frac{π}{4}$≤θ≤$\frac{π}{3}$,
∴-$\frac{π}{8}$≤$\frac{π}{8}$+θ≤$\frac{11π}{24}$,
∴$f({\frac{π}{16}})$=cos(2×$\frac{π}{16}$+θ)=cos($\frac{π}{8}$+θ)≤1.
故答案为:1.
点评 本题主要考查了三角函数恒等变换的应用,余弦函数的图象和性质的应用,考查了数形结合思想,属于基础题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
17.若幂函数f(x)=xα经过点$(2,\sqrt{2})$,则f(x)是( )
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)是减函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |
14.椭圆4x2+9y2=144内有一点P(3,2),则以P为中点的弦所在直线的斜率为( )
| A. | $-\frac{2}{3}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{4}{9}$ | D. | $-\frac{9}{4}$ |
11.设a+b<0,且b>0,则下列不等式正确的是( )
| A. | b2>-ab | B. | a2<-ab | C. | a2<b2 | D. | a2>b2 |
16.曲线y=2x2-x在点(0,0)处的切线方程为( )
| A. | x+y=0 | B. | x-y=0 | C. | x-y+2=0 | D. | x+y+2=0 |
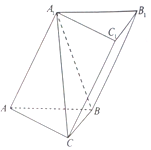 如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.
如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.