题目内容
9. 设抛物线E:y2=2px(p>0)上的点M(x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0.
设抛物线E:y2=2px(p>0)上的点M(x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0.(Ⅰ)求抛物线E的方程;
(Ⅱ)如图,直线l:y=k(x+2)与抛物线E交于A,B两点,点A关于x轴的对称点是C,求证:直线BC恒过一定点.
分析 (Ⅰ)根据抛物线的性质得出x0+$\frac{p}{2}$=$\frac{5}{4}$x0,得出M的坐标,代入抛物线方程求出p即可;
(Ⅱ)直线方程与抛物线方程联立,求出直线BC方程,即可得出结论.
解答 (Ⅰ)解:∵|MF|=x0+$\frac{p}{2}$=$\frac{5}{4}$x0,∴x0=2p.即M(2p,4).
把M(2p,4)代入抛物线方程得4p2=16,解得p=2.
∴抛物线Γ的方程为y2=4x.
(Ⅱ)证明:由题意,设A(x1,y1),B(x2,y2),C(x1,-y1) (x1≠x2).
由直线代入抛物线方程,消y整理得ky2-4y+8k=0,
则y1y2=8.
直线BC:y+y1=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$(x-x1)=$\frac{4}{{y}_{2}-{y}_{1}}$(x-x1),
所以y=$\frac{4}{{y}_{2}-{y}_{1}}$(x-x1$\frac{{y}_{2}{y}_{1}-{{y}_{1}}^{2}}{4}$)-,
所以y=$\frac{4}{{y}_{2}-{y}_{1}}$(x-2).
∴直线BC恒过定点(2,0).
点评 本题考查抛物线的方程,考查抛物线的简单几何性质、直线与圆锥曲线的综合问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,x<0}\\{\frac{1}{x},x>0}\end{array}\right.$的图象上存在不同的两点 A,B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (2,+∞) | C. | $({-∞,-2})∪({\frac{1}{4},+∞})$ | D. | $({-∞,\frac{1}{4}})$ |
17.若幂函数f(x)=xα经过点$(2,\sqrt{2})$,则f(x)是( )
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)是减函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |
4.设正实数x,y满足log${\;}_{\frac{1}{2}}$x+log2y=m(m∈[-1,1]),若不等式(x+y)2≤2ax2+(a+1)y2有解,则实数a的取值范围是( )
| A. | a≥1 | B. | a≥$\frac{8}{9}$ | C. | a≥$\frac{7}{8}$ | D. | a≥$\frac{5}{6}$ |
14.椭圆4x2+9y2=144内有一点P(3,2),则以P为中点的弦所在直线的斜率为( )
| A. | $-\frac{2}{3}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{4}{9}$ | D. | $-\frac{9}{4}$ |
19.已知O,F分别为双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的中心和右焦点,点G,M分别在E的渐近线和右支,FG⊥OG,GM∥x轴,且|OM|=|OF|,则E的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $\sqrt{2}$ |
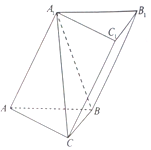 如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.
如图:在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AC=5,CB=3,AB=4,∠A1AB=60°.