题目内容
已知f（x）为R上的奇函数，当x∈[0，+∞）时，f（x）=x（1+x3），则f（-2）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据奇函数的性质得f（-2）=-f（2），代入已知的解析式求值即可．
解答：
解：因为f（x）为R上的奇函数，当x∈[0，+∞）时，f（x）=x（1+x3），
所以f（-2）=-f（2）=-2（1+8）=-18，
故答案为：-18．
所以f（-2）=-f（2）=-2（1+8）=-18，
故答案为：-18．
点评：本题考查奇函数的性质的应用，以及转化思想．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
下列四个正方体图形中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，则能得出AB∥平面MNP的图形个数是（ ）
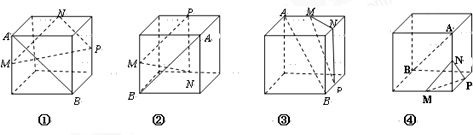
| A、1个 | B、2个 | C、3个 | D、4个 |
下列函数f（x）中，在（0，+∞）上为增函数的是（ ）
A、f（x）=
| ||
| B、f（x）=（x-1）2 | ||
| C、f（x）=lnx | ||
D、f（x）=(
|
设正方体ABCD-A1B1C1D1的棱长为1，则平面B1AC被正方体内切球截得图形的面积（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数x，y满足x2+y2-4x+6y+4=0，则
的最小值是（ ）
|
A、2
| ||
B、
| ||
C、
| ||
D、
|