题目内容
18.求下列不等式的解集.(1)-2x2+x<-3
(2)$\frac{x+1}{x-2}$≤2.
分析 (1)利用因式分解法即可求出,
(2)原不等式等价于(x-5)(x-2)≥0,且x-2≠2,解得即可
解答 解:(1))-2x2+x<-3等价于2x2-x-3>0,
即(2x-3)(x+1)<0,
解得x<-1或x>$\frac{3}{2}$,
故不等式的解集为{x|x<-1或x>$\frac{3}{2}$},
(2)$\frac{x+1}{x-2}$≤2等价于$\frac{x+1}{x-2}$-2≤0,
即$\frac{x-5}{x-2}$≥0,
即(x-5)(x-2)≥0,且x-2≠2,
解得x<2或x≥5,
故不等式的解集为{x|x<2或x≥5}
点评 本题考查了一元二次不等式和分式不等式的解法,属于基础题

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
3.已知$α,β∈(0,\frac{π}{2})$,则下列不等式一定成立的是( )
| A. | sin(α+β)<sinα+sinβ | B. | sin(α+β)>sinα+sinβ | ||
| C. | cos(α+β)<sinα+sinβ | D. | cos(α+β)>cosα+cosβ |
8.一个几何体的三视图如图所示,则该几何体表面积与其外接球的表面积之比为( )
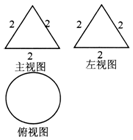

| A. | 3:4 | B. | 3:8 | C. | 3:16 | D. | 9:16 |
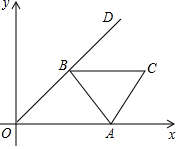 如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.
如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.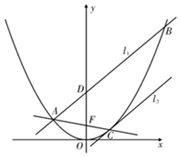 如图,已知过抛物线E:x2=4y的焦点F的直线交抛物线E与A、C两点,经过点A的直线l1分别交y轴、抛物线E于点D、B(B与C不重合),∠FAD=∠FDA,经过点C作抛物线E的切线为l2.
如图,已知过抛物线E:x2=4y的焦点F的直线交抛物线E与A、C两点,经过点A的直线l1分别交y轴、抛物线E于点D、B(B与C不重合),∠FAD=∠FDA,经过点C作抛物线E的切线为l2.