题目内容
13.条件p:|x+1|>2;条件q:{x|2<x<3},则?p是?q的( )| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
分析 利用不等式的解法、简易逻辑的判定方法即可得出.
解答 解:条件p:|x+1|>2,解得x>1或x<-3.可得¬p:[-3,1].
条件q:{x|2<x<3},¬q:(-∞,2]∪[3,+∞).
则?p是?q的充分不必要条件.
故选:C.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
16.将函数$y=sin(x-\frac{π}{3})$的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移$\frac{π}{3}$个单位,所得图象的解析式是( )
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
18.直线x+2y=m(m>0)与⊙O:x2+y2=5交于A,B两点,若|${\overrightarrow{OA}$+$\overrightarrow{OB}}$|>2|${\overrightarrow{AB}}$|,则m的取值范围是( )
| A. | $({\sqrt{5},2\sqrt{5}})$ | B. | $({2\sqrt{5},5})$ | C. | $({\sqrt{5},5})$ | D. | $({2,\sqrt{5}})$ |
5.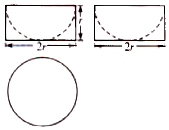 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
2.一个几何体的三视图如图所示,其中俯视图为正方形,则最长侧棱(不包括底面的棱)的长度为( )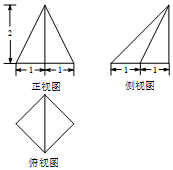

| A. | 2 | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
3.已知$α,β∈(0,\frac{π}{2})$,则下列不等式一定成立的是( )
| A. | sin(α+β)<sinα+sinβ | B. | sin(α+β)>sinα+sinβ | ||
| C. | cos(α+β)<sinα+sinβ | D. | cos(α+β)>cosα+cosβ |
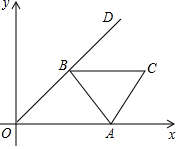 如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.
如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.