题目内容
8．已知$p：|{1-\frac{x-1}{3}}|$＜2；q：x2-2x+1-m2＜0，若?p是?q的充分非必要条件，求实数m的取值范围．分析 $|{1-\frac{x-1}{3}}|$＜2?-2＜x＜10，记A={x|-2＜x＜10}，B={x|x2-2x+1-m2＜0}，由?p是?q的充分非必要条件，可知：B?A．再利用二次函数的图象与性质即可得出．
解答 解：$|{1-\frac{x-1}{3}}|$＜2?-2＜x＜10，…（2分）
记A={x|-2＜x＜10}，
B={x|x2-2x+1-m2＜0}，
由?p是?q的充分非必要条件，可知：B?A…（4分）
记，f（x）=x2-2x+1-m2，则$\left\{\begin{array}{l}f（-2）≥0\\ f（10）≥0.\end{array}\right.$，即$\left\{\begin{array}{l}9-{m^2}≥0\\ 81-{m^2}≥0.\end{array}\right.$
解此不等式组得，-3≤m≤3…（8分）
经检验m=±3时上等式组中两不等式的等号不同时成立．
∴m的取值范围是-3≤m≤3…（10分）
点评 本题考查了不等式的解法、简易逻辑的判定方法、二次函数的图象与性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．复数z=i（-1+3i）在复平面上对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
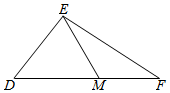如图所示，在△DEF中，M是在线段DF上，DE=3，DM=EM=2，sin∠F=$\frac{3}{5}$=，则边EF的长为$\frac{5\sqrt{7}}{4}$．
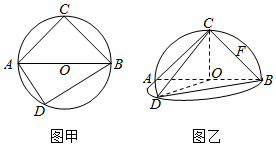如图甲：⊙O的直径AB=2，圆上两点C，D在直径AB的两侧，使∠CAB=$\frac{π}{4}$，∠DAB=$\frac{π}{3}$，沿直径AB折起，使两个半圆所在的平面互相垂直（如图乙），F为BC的中点，根据图乙解答下列各题：
17．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为4π，且对?x∈R，有f（x）≤f（$\frac{π}{3}$）成立，则f（x）的一个对称中心坐标是（ ）
| A． | （-$\frac{2π}{3}$，0） | B． | （-$\frac{π}{3}$，0） | C． | （$\frac{2π}{3}$，0） | D． | （$\frac{5π}{3}$，0） |