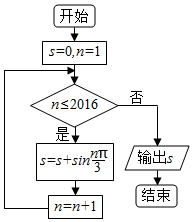
题目内容
16．若（x-$\frac{a}{x}$）6展开式的常数项为20，则常数a的值为-1．分析 在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项，再根据常数项等于20，求得实数a的值．
解答 解：（x-$\frac{a}{x}$）6展开式的通项公式为Tr+1=${C}_{6}^{r}$•（-a）r•x6-2r，令6-2r=0，求得r=3，
可得它的常数项为${C}_{6}^{3}$•（-a3）=20，则常数a=-1，
故答案为：-1．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
1．“xy≠0”是“x≠0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
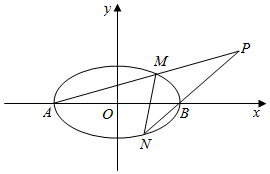已知椭圆E：$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A，B，M，N是椭圆E上异于A，B的两点，直线AM，BN交于点P（4，t）．