若x在第三象限.化简$\sqrt{{}^{2}{+}^{2}}$．题目和参考答案——青夏教育精英家教网——

题目内容

17．若x在第三象限，化简$\sqrt{{（1+tanx）}^{2}{+（1-tanx）}^{2}}$．

分析根据同角三角函数的关系和象限角的符号化简即可．

解答解：∵x在第三象限，
∴$\sqrt{{（1+tanx）}^{2}{+（1-tanx）}^{2}}$=$\sqrt{2（1+ta{n}^{2}x）}$=$\sqrt{2}$•$\sqrt{1+\frac{si{n}^{2}α}{co{s}^{2}α}}$=$\sqrt{2}$•$\frac{1}{\sqrt{co{s}^{2}α}}$=$\frac{\sqrt{2}}{|cosα|}$=-$\frac{\sqrt{2}}{cosα}$

点评本题考查了同角三角函数的关系，以及象限角的符号，属于基础题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

7．已知（1+x+x²）（1-x）⁵=a₀+a₁x+a₂x²+…+a₇x⁷，则|a₁|+|a₂|+…+|a₇|=31．

8．已知向量|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°．
（1）求$\overrightarrow{a}$•$\overrightarrow{b}$；
（2）若$\overrightarrow{c}$=2$\overrightarrow{a}$-$\overrightarrow{b}$，$\overrightarrow{d}$=$\overrightarrow{a}$+$λ\overrightarrow{b}$，且$\overrightarrow{c}$⊥$\overrightarrow{d}$，求实数λ的值．

5．点（-1，3）关于直线y=-x的对称点是（-3，1）．

12．已知数列{a_n}中a₁=1，S_n=4a_n-1+2，
（1）求a₂，a₃；
（2）设b_n=a_n+1-2a_n，求数列{b_n}的通项公式b_n．

4．已知三棱柱ABC-A′B′C′的底面为直角三角形，两条直角边AC和BC的长分别为4和3，侧棱AA′的长为10．
（1）若侧棱AA′垂直于底面，求该三棱柱的表面积；
（2）若侧棱AA′与底面所成的角为60°，求该三棱柱的体积．

11．已知F₁、F₂是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左、右焦点，P是椭圆上一点（异于左、右顶点），过点P作∠F₁PF₂的角平分线交x轴于点M，若2|PM|²=|PF₁|•|PF₂|，则椭圆的离心率为$\frac{\sqrt{2}}{2}$．

8．已知$p：|{1-\frac{x-1}{3}}|$＜2；q：x²-2x+1-m²＜0，若?p是?q的充分非必要条件，求实数m的取值范围．

9．如图所示的程序框图，输出S的值为（　　）

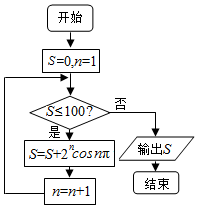
$\frac{{{2^{99}}-2}}{3}$

$\frac{{{2^{100}}-2}}{3}$

$\frac{{{2^{101}}-2}}{3}$

$\frac{{{2^{102}}-2}}{3}$