题目内容
13.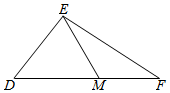 如图所示,在△DEF中,M是在线段DF上,DE=3,DM=EM=2,sin∠F=$\frac{3}{5}$=,则边EF的长为$\frac{5\sqrt{7}}{4}$.
如图所示,在△DEF中,M是在线段DF上,DE=3,DM=EM=2,sin∠F=$\frac{3}{5}$=,则边EF的长为$\frac{5\sqrt{7}}{4}$.
分析 在△DEM中使用余弦定理解出cosD,得到sinD,在△DEF中使用正弦定理解出EF.
解答 解:在△DEM中,由余弦定理得cos∠DME=$\frac{D{M}^{2}+E{M}^{2}-D{E}^{2}}{2DM•EM}$=-$\frac{1}{8}$.
∴sin∠EMF=sin∠DME=$\sqrt{1-co{s}^{2}∠DME}$=$\frac{\sqrt{63}}{8}$.
在△EMF中,由正弦定理得$\frac{EM}{sinF}=\frac{EF}{sin∠EMF}$,即$\frac{2}{\frac{3}{5}}=\frac{EF}{\frac{\sqrt{63}}{8}}$,
解得EF=$\frac{5\sqrt{7}}{4}$.
故答案为$\frac{5\sqrt{7}}{4}$.
点评 本题考查了正余弦定理在解三角形中的应用,选择合适的三角形是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.“xy≠0”是“x≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.已知i为虚数单位,则z=$\frac{i}{1-2i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.在2015年全国青运会火炬传递活动中,有编号为1,2,3,4,5的5名火炬手.若从中任选2人,则选出的火炬手的编号相连的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{10}$ | D. | $\frac{2}{5}$ |
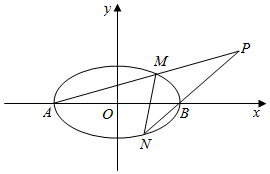 已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).
已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).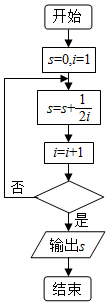 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图,其中菱形判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图,其中菱形判断框内应填入的条件是( )