题目内容
20.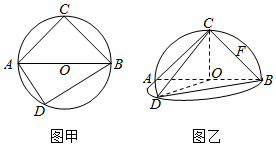 如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题:
如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题:(Ⅰ)若点G是$\widehat{BD}$的中点,证明:FG∥平面ACD;
(Ⅱ)求平面ACD与平面BCD所成的锐二面角的余弦值.
分析 (1)根据线面平行的判定定理进行证明即可;
(2)建立空间直角坐标系,利用向量法表示出E的坐标,求出平面的法向量,利用向量法进行求解即可.
解答 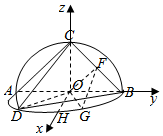 (Ⅰ)证明:连接OF,FG,OG,
(Ⅰ)证明:连接OF,FG,OG,
∵F,O是BC,AB的中点,
∴FO∥AC,
∵FO?平面ACD,AC?平面ACD,
∴FO∥平面ACD,
∵∠DAB=$\frac{π}{3}$,且G是BD弧的中点,
∴∠BOG=$\frac{π}{3}$,则AD∥OG,
∵OG?平面ACD,AD?平面ACD,
∴OG∥平面ACD,
∵FO∩OG=O,FO,OG?平面FOG,
∴面FOG∥面ACD,
又FG?平面FOG,
∴FG∥平面ACD
(Ⅱ)如图,设H为弧DG的中点,建立以O为坐标原点,OH,OB,OC分别为x,y,z轴的空间直角坐标系如图:
则A(0,-1,0),B(0,1,0),C(0,0,1),D($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),G($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),
设平面ACD的法向量为$\overrightarrow{m}$=(x,y,z),则$\overrightarrow{AC}$=(0,1,1),$\overrightarrow{AD}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),
则由$\overrightarrow{m}$•$\overrightarrow{AC}$=y+z=0,$\overrightarrow{m}$•$\overrightarrow{AD}$=$\frac{\sqrt{3}}{2}$x+$\frac{1}{2}$y=0,得$\left\{\begin{array}{l}{z=-y}\\{x=-\frac{\sqrt{3}}{3}y}\end{array}\right.$,
令y=-$\sqrt{3}$,则$\overrightarrow{m}$=(1,-$\sqrt{3}$,$\sqrt{3}$),
同理可得平面BCD的法向量为$\overrightarrow{n}$=($\sqrt{3}$,1,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\sqrt{3}}{\sqrt{7}×\sqrt{5}}$=$\frac{\sqrt{105}}{35}$,
即平面ACD与平面BCD所成的锐二面角的余弦值是$\frac{\sqrt{105}}{35}$.
点评 本题主要考查线面平行的判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.

 走进文言文系列答案
走进文言文系列答案| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
| A. | $\frac{{{2^{99}}-2}}{3}$ | B. | $\frac{{{2^{100}}-2}}{3}$ | C. | $\frac{{{2^{101}}-2}}{3}$ | D. | $\frac{{{2^{102}}-2}}{3}$ |
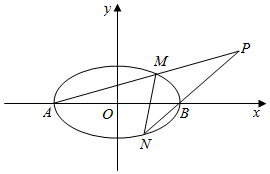 已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).
已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).