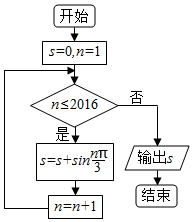
题目内容
18.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右顶点分别为A,B,右焦点为F,离心率$e=\frac{1}{2}$,点P是椭圆C上异于A,B两点的动点,△APB的面积最大值为$2\sqrt{3}$.(1)求椭圆C的方程;
(2)若直线AP与直线x=2交于点D,试判断以BD为直径的圆与直线PF的位置关系,并作出证明.
分析 (1)运用椭圆的离心率公式和a,b,c的关系,以及椭圆上点到x轴距离的最大值,计算即可得到a,b的值,进而得到椭圆方程;
(2)以BD为直径的圆与直线PF相切.设直线AP:y=k(x+2)(k≠0),代入椭圆方程,运用韦达定理,可得P的坐标,再由点到直线的距离公式和直线与圆相切的条件:d=r,即可得到结论.
解答 解:(1)由题意得,e=$\frac{c}{a}$=$\frac{1}{2}$,a2-b2=c2,
当P为椭圆的上顶点时,△APB的面积取得最大值
且为$\frac{1}{2}$•b•2a=$2\sqrt{3}$,
解得,a=2,b=$\sqrt{3}$,c=1,
所以椭圆方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)以BD为直径的圆与直线PF相切.
证明:设直线AP:y=k(x+2)(k≠0),
可得D(2,4k),BD的中点为M为(2,2k)
联立$\left\{\begin{array}{l}{y=k(x+2)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,消去y整理得,
(3+4k2)x2+16k2x+16k2-12=0,
设P(x0,y0),由韦达定理得,$-2{x_0}=\frac{{16{k^2}-12}}{{3+4{k^2}}}$,
解得,${x_0}=\frac{{6-8{k^2}}}{{3+4{k^2}}}$,
故有,${y_0}=k({{x_0}+2})=\frac{12k}{{3+4{k^2}}}$,
又F(1,0),所以当$k=±\frac{1}{2}$时,$P({1,±\frac{3}{2}})$,D(2,±2),此时PF⊥x轴,
以BD为直径的圆(x-2)2+(y±1)2=1与直线PF相切;
当$k≠±\frac{1}{2}$时,${k_{PF}}=\frac{y_0}{{{x_0}-1}}=\frac{4k}{{1-4{k^2}}}$,
所以直线PF:$y=\frac{4k}{{1-4{k^2}}}({x-1})$,即$\frac{4k}{{1-4{k^2}}}x-y-\frac{4k}{{1-4{k^2}}}=0$,
所以点E到直线PF的距离d=$\frac{|\frac{8k}{1-{k}^{2}}-2k-\frac{4k}{1-{4k}^{2}}|}{\sqrt{(\frac{4k}{1-4{k}^{2}})^{2}+1}}$=2|k|,
而BD=4k,即知d=$\frac{1}{2}$|BD|,所以以BD为直径的圆与直线PF相切.
点评 本题考查椭圆的方程的求法,注意运用椭圆的离心率公式和椭圆的性质,考查直线方程和椭圆方程联立,运用判别式大于0和韦达定理,同时考查直线和圆的位置关系,点到直线的距离公式和相切的条件,属于中档题.

| A. | $\frac{{{2^{99}}-2}}{3}$ | B. | $\frac{{{2^{100}}-2}}{3}$ | C. | $\frac{{{2^{101}}-2}}{3}$ | D. | $\frac{{{2^{102}}-2}}{3}$ |
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
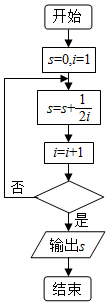 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图,其中菱形判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图,其中菱形判断框内应填入的条件是( )| A. | i>5 | B. | i<5 | C. | i>6 | D. | i<6 |
| A. | p∧q | B. | ¬p∨q | C. | p∨q | D. | ¬p∧q |