题目内容
12.设抛物线Γ:x2=2py(p>0)的准线被圆O:x2+y2=4所截得的弦长为$\sqrt{15}$(Ⅰ)求抛物线Γ的方程;
(Ⅱ)设点F是抛物线Γ的焦点,N为抛物线Γ上的一动点,过N作抛物线Γ的切线交圆O于P、Q两点,求△FPQ面积的最大值.
分析 (Ⅰ)求出抛物线的准线方程,利用直线与圆的位置关系列出方程,求出P即可求抛物线Γ的方程;
(Ⅱ)设N(t,$\frac{{t}^{2}}{2}$),圆心O到直线PQ的距离为$\frac{\frac{{t}^{2}}{2}}{\sqrt{1+{t}^{2}}}$,求出点F到直线PQ的距离,表示出△FPQ面积,利用配方法,可求△FPQ面积的最大值.
解答 解:(Ⅰ)因为抛物线Γ的准线方程为:y=-$\frac{p}{2}$,
且直线被圆O:x2+y2=4所截得的弦长为$\sqrt{15}$,
所以$\sqrt{4-(\frac{p}{2})^{2}}$=$\frac{1}{2}$$\sqrt{15}$解得p=1,
因此抛物线Γ的方程为x2=2y…(4分).
(Ⅱ)设N(t,$\frac{{t}^{2}}{2}$),由y′=x知直线PQ的方程为:y-$\frac{{t}^{2}}{2}$=t(x-t).即y=tx-$\frac{{t}^{2}}{2}$.(6分)
因为圆心O到直线PQ的距离为$\frac{\frac{{t}^{2}}{2}}{\sqrt{1+{t}^{2}}}$,所以|PQ|=2$\sqrt{4-\frac{{t}^{4}}{4(1+{t}^{2})}}$,(7分)
设点F到直线PQ的距离为d,则d=$\frac{\frac{1}{2}+\frac{{t}^{2}}{2}}{\sqrt{1+{t}^{2}}}$=$\frac{1}{2}\sqrt{1+{t}^{2}}$,( 8分)
所以,△FPQ的面积S=$\frac{1}{2}$|PQ|d=$\frac{1}{4}$$\sqrt{-{t}^{4}+16{t}^{2}+16}$=$\frac{1}{4}$$\sqrt{-({t}^{2}-8)^{2}+80}$≤$\sqrt{80}$=$\sqrt{5}$(11分)
当t=±2$\sqrt{2}$时取到“=”,经检验此时直线PQ与圆O相交,满足题意.
综上可知,△FPQ的面积的最大值为$\sqrt{5}$.(12分).
点评 本题考查直线与圆的位置关系,考查抛物线方程,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案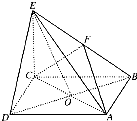 四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.
四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.