题目内容
12．已知方程x2+bx+c=0的两实根为-1和3，（1）求b与 c；
（2）解不等式：x2+bx+c＞0．
分析 （1）由题意，利用根与系数的关系即可求出b、c的值；
（2）把b、c的值代入不等式，解一元二次不等式即可．
解答 解：（1）由方程x2+bx+c=0的两实根为-1和3，
利用根与系数的关系得
$\left\{\begin{array}{l}{-b=-1+3}\\{c=-1×3}\end{array}\right.$，
解得b=-2，c=-3；
（2）b=-2，c=-3时，原不等式为x2-2x-3＞0，
即（x+1）（x-3）＞0，
解得x＜-1或x＞3；
所以不等式的解集为（-∞，-1）∪（3，+∞）．
点评 本题考查了一元二次不等式与对应方程的应用问题，是基础题目．
练习册系列答案
科学实验活动册系列答案
相关题目
2．
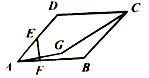如图所示，四边形ABCD是菱形，边长为2，∠BAD=60°，E为边AD的中点，点F在边AB上运动，点A关于直线EF的对称点为G，则线段CG的长度最小值为（ ）
如图所示，四边形ABCD是菱形，边长为2，∠BAD=60°，E为边AD的中点，点F在边AB上运动，点A关于直线EF的对称点为G，则线段CG的长度最小值为（ ）| A． | $\sqrt{7}-1$ | B． | 2 | C． | $\sqrt{5}-1$ | D． | $\sqrt{3}$ |
7．已知函数y=2cosx的定义域为[$\frac{π}{3}$，$\frac{4π}{3}$]，值域为[a，b]，则b-a的值是（ ）
| A． | 2 | B． | 3 | C． | $\sqrt{3}$+2 | D． | $2\sqrt{3}$ |
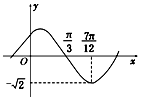（1）求$f（x）=tan（3x-\frac{π}{4}）$的定义域