题目内容
17.已知sin(π+α)=$\frac{3}{5}$且α是第三象限的角,则cos(α-2π)的值是( )| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
分析 利用同角三角函数的基本关系,诱导公式,以及三角函数在各个象限中的符号,求得cos(α-2π)的值.
解答 解:∵sin(π+α)=-sinα=$\frac{3}{5}$,∴sinα=-$\frac{3}{5}$,∵α是第三象限的角,则cos(α-2π)=cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{4}{5}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系,诱导公式,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
4.已知函数f(x)的导函数为f'(x),对一切的x∈R都有f'(x)>f(x)成立,对任意正数a,b,若a<b,则有( )
| A. | bf(lna)<af(lnb) | B. | bf(lna)=af(lnb) | ||
| C. | bf(lna)>af(lnb) | D. | bf(lna)与af(lnb)的大小不确定 |
2.已知函数f(x)=$\left\{\begin{array}{l}{x,x≤0}\\{{x}^{2}-x,x>0}\end{array}\right.$,若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( )
| A. | $({-\frac{1}{4},0})$ | B. | $({-\frac{1}{4},0}]$ | C. | $[{-\frac{1}{2},1}]$ | D. | $[{-\frac{1}{2},1})$ |
7.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-2x+2,x≤2\\{log_2}x,x>2\end{array}\right.$,若?x0∈R,使得$f({x_0})≤5m-4{m^2}$成立,则实数m的取值范围为( )
| A. | $[{-1,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},1}]$ | C. | $[{-2,\frac{1}{4}}]$ | D. | $[{\frac{1}{3},1}]$ |
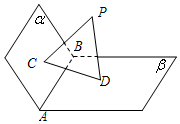 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.