题目内容
4.已知函数f(x)的导函数为f'(x),对一切的x∈R都有f'(x)>f(x)成立,对任意正数a,b,若a<b,则有( )| A. | bf(lna)<af(lnb) | B. | bf(lna)=af(lnb) | ||
| C. | bf(lna)>af(lnb) | D. | bf(lna)与af(lnb)的大小不确定 |
分析 由题意可知f'(x)-f(x)>0,构造辅助函数,求导,则g(x)在(-∞,+∞)上单调递增,由lna<lnb,则g(lna)<g(lnb),即可求得bf(lna)<af(lnb).
解答 解:由f'(x)>f(x),即f'(x)-f(x)>0,
设g(x)=$\frac{f(x)}{{e}^{x}}$,g(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$>0,
∴g(x)在(-∞,+∞)上单调递增,
由任意正数a,b,且a<b,则lna<lnb,
∴g(lna)<g(lnb),则$\frac{f(lna)}{a}$<$\frac{f(lnb)}{b}$,
∴bf(lna)<af(lnb),
故选A.
点评 本题考查导数的综合应用,考查利用导数研究函数的单调性,考查转化思想,属于中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
14.已知$|{\vec b}|=3$,$\vec a$在$\vec b$方向上的投影为$\frac{3}{2}$,则$\vec a$•$\vec b$=( )
| A. | 2 | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
12.△ABC中,c是a与b的等差中项,sinA,sinB,sinC依次为一等比数列的前n项,前2n项,前3n项的和,则cosC的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
17.已知sin(π+α)=$\frac{3}{5}$且α是第三象限的角,则cos(α-2π)的值是( )
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
18.随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
(Ⅰ)若以“年龄45岁为分界点”.由以上统计数据完成下面的2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关:
(Ⅱ)若从年龄在,总有g(x1)<f (x2)成立,其中e=2.71828…是自然对数的底数.
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
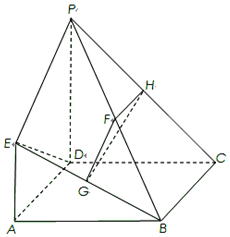 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.