题目内容
过椭圆
+
=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,那么“左特征点”M一定是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、椭圆左准线与x轴的交点 |
| B、坐标原点 |
| C、椭圆右准线与x轴的交点 |
| D、右焦点 |
考点:椭圆的简单性质
专题:新定义,圆锥曲线的定义、性质与方程
分析:设出点M(m,0)为椭圆的左特征点,根据椭圆左焦点,设出直线AB的方程代入椭圆方程,由∠AMB被x轴平分,得kAM+kBM=0,利用韦达定理,求出结论.
解答:
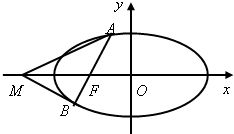 解:如图所示,设M(m,0)为椭圆
解:如图所示,设M(m,0)为椭圆
+
=1的左特征点,椭圆的左焦点F(-c,0),
可设直线AB的方程为x=ky-c(k≠0)
代入椭圆
+
=1,得:b2(ky-c)2+a2y2=a2b2,
即(a2+b2k2)y2-2kcb2y+b2c2-a2b2=0,
(a2+b2k2)y2-2kcb2y-b4=0,
设A(x1,y1),B(x2,y2)
得y1+y2=
,y1y2=-
∵∠AMB被x轴平分,kAM+kBM=0,即
+
=0,
即y1(ky2-c)+y2(ky1-c)-(y1+y2)m=0,
∴2ky1y2-(y1+y2)(m+c)=0,
∴2k•(-
)-
•(m+c)=0
∵k≠0,∴b2+c(m+c)=0,
即m=-
-c=-
,
∴M(-
,0);
即点M是椭圆左准线与x轴的交点.
故选:A.
 解:如图所示,设M(m,0)为椭圆
解:如图所示,设M(m,0)为椭圆| x2 |
| a2 |
| y2 |
| b2 |
可设直线AB的方程为x=ky-c(k≠0)
代入椭圆
| x2 |
| a2 |
| y2 |
| b2 |
即(a2+b2k2)y2-2kcb2y+b2c2-a2b2=0,
(a2+b2k2)y2-2kcb2y-b4=0,
设A(x1,y1),B(x2,y2)
得y1+y2=
| 2kcb2 |
| a2+b2k2 |
| b4 |
| a2+b2k2 |
∵∠AMB被x轴平分,kAM+kBM=0,即
| y1 |
| x1-m |
| y2 |
| x2-m |
即y1(ky2-c)+y2(ky1-c)-(y1+y2)m=0,
∴2ky1y2-(y1+y2)(m+c)=0,
∴2k•(-
| b4 |
| a2+b2k2 |
| 2kcb2 |
| a2+b2k2 |
∵k≠0,∴b2+c(m+c)=0,
即m=-
| b2 |
| c |
| a2 |
| c |
∴M(-
| a2 |
| c |
即点M是椭圆左准线与x轴的交点.
故选:A.
点评:本题考查了椭圆性质的应用问题以及直线与椭圆相交关系的处理问题,解题时应灵活设出直线AB的方程,以避免讨论直线的斜率是否存在,是中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
若方程2x2+4x+1=0,则|x2-x1|=( )
A、-
| ||
B、±
| ||
C、
| ||
| D、0 |
点A是曲线C1:
+
=1与C2:
-y2=1的一个交点,点A到曲线C1两焦点距离的和为m,点A到曲线C2两焦点距离之差的绝对值为n,则lg
的值为( )
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| 4 |
| 1 |
| m+n |
| A、0 | B、-1 | C、1 | D、10 |
曲线y=xn(n∈N)在点P(
,2
)处切线斜率为20,那么n为( )
| 2 |
| n |
| 2 |
| A、7 | B、6 | C、5 | D、4 |
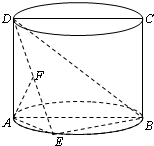 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上(点E异于A、B两点),点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上(点E异于A、B两点),点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π. 如图是某研究性学习小组对全班50人的情商进行调查,按照区间进行分组,得到的情商的分布图,则情商在90-105的人数为
如图是某研究性学习小组对全班50人的情商进行调查,按照区间进行分组,得到的情商的分布图,则情商在90-105的人数为