题目内容
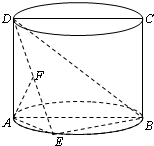 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上(点E异于A、B两点),点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上(点E异于A、B两点),点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.(1)求证:AF⊥BD;
(2)求直线DE与平面ABCD所成角的正切值.
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)欲证AF⊥DB,先证AF⊥平面DEB,根据线面垂直的判定定理可知只需证EB⊥AF,AF⊥DE,且EB∩DE=E,即可证得线面垂直;
(2)点E作EH⊥AB,H是垂足,连接DH,易证∠EDH是DE与平面ABCD所成的角,在三角形EDH中求出此角即可.
(2)点E作EH⊥AB,H是垂足,连接DH,易证∠EDH是DE与平面ABCD所成的角,在三角形EDH中求出此角即可.
解答:
(1)证明:根据圆柱性质,DA⊥平面ABE.
∵EB?平面ABE,
∴DA⊥EB.
∵AB是圆柱底面的直径,点E在圆周上,
∴AE⊥EB,又AE∩AD=A,
故得EB⊥平面DAE.
∵AF?平面DAE,
∴EB⊥AF.
又AF⊥DE,且EB∩DE=E,
故得AF⊥平面DEB.
∵DB?平面DEB,
∴AF⊥DB.
(2)∵平面ABCD⊥面ABE,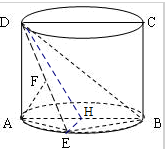
∴过E作EH⊥AB,
则EH⊥面ABCD,
即∠EDH为DE与平面ABCD所成角,
设圆柱的底半径为r,因为圆柱的轴截面ABCD是正方形,
△ABE的面积为S=
•AB•EH=r•EH.圆柱的底面积S=π•r2,
∵若圆柱的底面积与△ABE的面积之比等于π,
∴r•EH•π=π•r2,
解得EH=r,
∴点H为圆柱底面圆的圆心,
则tan∠EDH=
=
=
=
,
即直线DE与平面ABCD所成角的正切值
.
∵EB?平面ABE,
∴DA⊥EB.
∵AB是圆柱底面的直径,点E在圆周上,
∴AE⊥EB,又AE∩AD=A,
故得EB⊥平面DAE.
∵AF?平面DAE,
∴EB⊥AF.
又AF⊥DE,且EB∩DE=E,
故得AF⊥平面DEB.
∵DB?平面DEB,
∴AF⊥DB.
(2)∵平面ABCD⊥面ABE,

∴过E作EH⊥AB,
则EH⊥面ABCD,
即∠EDH为DE与平面ABCD所成角,
设圆柱的底半径为r,因为圆柱的轴截面ABCD是正方形,
△ABE的面积为S=
| 1 |
| 2 |
∵若圆柱的底面积与△ABE的面积之比等于π,
∴r•EH•π=π•r2,
解得EH=r,
∴点H为圆柱底面圆的圆心,
则tan∠EDH=
| EH |
| DH |
| r | ||
|
| 1 | ||
|
| ||
| 5 |
即直线DE与平面ABCD所成角的正切值
| ||
| 5 |
点评:本小题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力.要求熟练掌握相应的判定定理和线面角的求解方法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知函数f(x)=log
(4x-2x+1+1)的值域是[0,+∞),则它的定义域可以是( )
| 1 |
| 2 |
| A、(0,1] |
| B、(0,1) |
| C、(-∞,1] |
| D、(-∞,0] |
f′(x0)=0是可导函数y=f(x)在点x=x0处有极值的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
与双曲线x2-
=1有共同的渐近线,且过点(2,2)的双曲线方程为( )
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
过椭圆
+
=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,那么“左特征点”M一定是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、椭圆左准线与x轴的交点 |
| B、坐标原点 |
| C、椭圆右准线与x轴的交点 |
| D、右焦点 |
若P点在△ABC确定的平面上,O为平面外一点,下列说法中不正确的是( )
A、
| ||||||||||||||
B、若
| ||||||||||||||
C、
| ||||||||||||||
D、若P点是△ABC的重心,则
|