题目内容
已知数列{an}的通项公式an=2n-
,求an的前n项和Sn.
| n |
| 2n-1 |
考点:数列的求和
专题:等差数列与等比数列
分析:由数列的通项公式特点,应利用分组求和法、错位相减法求出前n项和Sn.
解答:
解:由题意得,an=2n-
,
所以{an}的前n项和Sn=(2+22+23+…+2n)-(
+
+
+…+
),
=
-(
+
+
+…+
)=2n+1-2-(
+
+
+…+
),
设S=
+
+
+…+
,①
则
S=
+
+
+…+
,②
①-②得,
S=
+
+
+
+…+
-
=
-
=2-
,
则S=4-
,
所以Sn=2n+1-2+4-
=2n+1+2-
.
| n |
| 2n-1 |
所以{an}的前n项和Sn=(2+22+23+…+2n)-(
| 1 |
| 20 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
=
| 2(1-2n) |
| 1-2 |
| 1 |
| 20 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 20 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
设S=
| 1 |
| 20 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
则
| 1 |
| 2 |
| 1 |
| 21 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
①-②得,
| 1 |
| 2 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| n |
| 2n |
=
1-
| ||
1-
|
| n |
| 2n |
| n+2 |
| 2n |
则S=4-
| n+2 |
| 2n-1 |
所以Sn=2n+1-2+4-
| n+2 |
| 2n-1 |
| n+2 |
| 2n-1 |
点评:本题主要考查等比数列的前n项和公式,以及分组求和法、错位相减法求数列的前n项和,考查运算求解能力,以及整合思想、化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
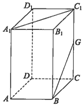
长方体ABCD-A1B1C1D1中,AA1=2AB=2AD,G为CC1中点,则直线A1C1与BG所成角的大小是( )

| A、30° | B、45° |
| C、60° | D、120° |
若na=2,log3b=
,c3=
(其中e为自然对数的底数),则a、b、c的大小关系正确的是( )
| 1 |
| e |
| 1 |
| 9 |
| A、b>a>c |
| B、c>b>a |
| C、b>c>a |
| D、a>b>c |
正方体ABCD-A1B1C1D1中,异面直线A1C1与B1C所成的角是( )
| A、30° | B、45° |
| C、60° | D、90° |
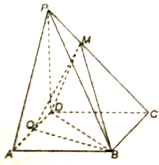 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PD⊥平面ABCD,∠BAD=60°,Q为AD中点,AD=4,PD=6.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PD⊥平面ABCD,∠BAD=60°,Q为AD中点,AD=4,PD=6.