Question

以M为圆心半径为2.5的圆外接于△ABC，且5

MA

+13

MC

+12

MB

=

0

，则两个面积比

S△BCM

S△ABM

=

 

．

Answer 1

考点：平面向量的基本定理及其意义

专题：平面向量及应用

分析：如图所示，分别延长MA，MB，MC，使得

MD

=5

MA

，

ME

=12

MB

，

MF

=13

MC

．由5

MA

+13

MC

+12

MB

=

0

，可得

MD

+

ME

+

MF

=

0

，延长点M是△DEF的重心．而

S△MBC

S△MEF

=

1×1

12×13

，可得S_△MBC=

1

12×13

S△MEF=

1

12×13

×

1

3

S△DEF，同理可得S_△MAB=

1

12×5

×

1

3

×S△DEF，即可得出．

解答： 解：如图所示，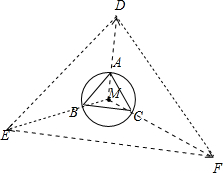
分别延长MA，MB，MC，使得

MD

=5

MA

，

ME

=12

MB

，

MF

=13

MC

．
∵5

MA

+13

MC

+12

MB

=

0

，
∴

MD

+

ME

+

MF

=

0

，
∴点M是△DEF的重心．
∵

S△MBC

S△MEF

=

1×1

12×13

，
∴S_△MBC=

1

12×13

S△MEF=

1

12×13

×

1

3

S△DEF，
同理可得S_△MAB=

1

12×5

×

1

3

×S△DEF，
∴

S△BCM

S△ABM

=

5

13

．
故答案为：

5

13

．

点评：本题考查了三角形的重心定理、三角形的面积之比，考查了推理能力与计算能力，属于中档题．