题目内容
函数f(x)=cos(2x-
)+2sin(x-
)sin(x+
)图象的对称轴方程是 .
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用两角差的余弦公式,诱导公式及二倍角正弦公式将f(x)化为一角一函数形式得出f(x)=sin(2x-
),将2x-
看作整体借助于正弦函数的对称轴方程求解.
| π |
| 6 |
| π |
| 6 |
解答:
解:f(x)=cos(2x-
)+2sin(x-
)sin(x+
)
=
cos2x+
sin2x+sin(2x-
)
=
cos2x+
sin2x-
cos2x
=-
cos2x+
sin2x
=sin(2x-
).
由2x-
=kπ+
,k∈Z得图象的对称轴方程 x=
+
,k∈Z
故答案为:x=
+
,(k∈Z).
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
| π |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| ||
| 2 |
=sin(2x-
| π |
| 6 |
由2x-
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 3 |
故答案为:x=
| kπ |
| 2 |
| π |
| 3 |
点评:本题考查利用三角公式进行恒等变形的技能以及运算能力,三角函数的图象和性质,考查了整体换元的思想方法,考查了转化思想,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知函数y=sin(2x+φ)在(
,
)上单调递增,其中φ∈(π,2π),则φ的取值范围为( )
| π |
| 4 |
| π |
| 3 |
A、[
| ||||
B、(π,
| ||||
C、[
| ||||
D、[
|
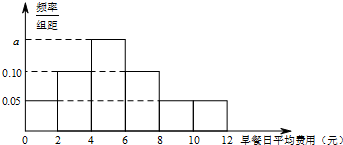 某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清.
某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清.