题目内容
长方体ABCD-A1B1C1D1中，AA1=2AB=2AD，G为CC1中点，则直线A1C1与BG所成角的大小是（ ）
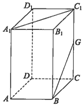
| A、30° | B、45° |
| C、60° | D、120° |
考点：异面直线及其所成的角
专题：空间角
分析：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出直线A1C1与BG所成角．
解答：
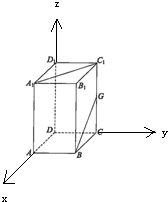解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，
建立空间直角坐标系，
设AA1=2AB=2AD=2，
A1（1，0，2），C1（0，1，2），
=（-1，1，0），
B（1，1，0），G（0，1，1），
=（-1，0，1），
设直线A1C1与BG所成角为θ，
cosθ=
=
=
，
∴θ=60°．
故选：C．
解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，
设AA1=2AB=2AD=2，
A1（1，0，2），C1（0，1，2），
| A1C1 |
B（1，1，0），G（0，1，1），
| BG |
设直线A1C1与BG所成角为θ，
cosθ=
|
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
∴θ=60°．
故选：C．
点评：本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力，解题时要注意向量法的合理运用．
练习册系列答案
相关题目
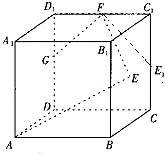如图，已知正方体ABCD-A1B1C1D1的棱长为2，点E是正方形BCC1B1的中心，点F，G分别是棱C1D1，DD1的中点．设点E1是点E在平面DCC1D1内的正投影．