题目内容
5.已知R是实数集,集合 A={x|22x+1≥16},B={x|(x-1)(x-3)<0,则(∁RA)∩B=( )| A. | (1,2) | B. | [1,2] | C. | (1,3) | D. | (1,$\frac{3}{2}$) |
分析 运用指数不等式和二次不等式的解法,可得集合A,B,求出∁RA,再由交集的定义,即可得到所求集合.
解答 解:集合 A={x|22x+1≥16}={x|22x+1≥24}={x|2x+1≥4}={x|x≥$\frac{3}{2}$},
B={x|(x-1)(x-3)<0}={x|1<x<3},
∁RA={x|x<$\frac{3}{2}$},
可得(∁RA)∩B={x|1<x<$\frac{3}{2}$}=(1,$\frac{3}{2}$).
故选:D.
点评 本题考查集合的运算,主要是交集和补集的求法,同时考查指数不等式和二次不等式的解法,运用定义法解题是关键,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20.已知函数f(x)=(sinx+cosx)cosx,则下列说法正确的为( )
| A. | 函数f(x)的最小正周期为2π | |
| B. | f(x)在[$\frac{5π}{8}$,$\frac{9π}{8}$]单调递减 | |
| C. | f(x)的图象关于直线x=-$\frac{π}{6}$对称 | |
| D. | 将f(x)的图象向右平移$\frac{π}{8}$,再向下平移$\frac{1}{2}$个单位长度后会得到一个奇函数的图象 |
10.在平面直角坐标系内,区域M满足$\left\{\begin{array}{l}0≤x≤π\\ 0≤y≤1\end{array}$区域N满足$\left\{\begin{array}{l}0≤x≤π\\ 0≤y≤sinx\end{array}$则向区域M内投一点,落在区域N内的概率是( )
| A. | $\frac{2}{π}$ | B. | $\frac{π}{4}$ | C. | 2-$\frac{2}{π}$ | D. | 2-$\frac{π}{4}$ |
14.已知正方形ABCD的边长为2,E是BC的中点,以点C为圆心,CE长为半径作圆,点P是该圆上的任一点,则$\overrightarrow{AP}•\overrightarrow{DE}$的取值范围是( )
| A. | $[0,2+\sqrt{6}]$ | B. | $[2-\sqrt{6},2+\sqrt{6}]$ | C. | $[0,2+\sqrt{5}]$ | D. | $[2-\sqrt{5},2+\sqrt{5}]$ |
15.若圆C与y轴相切于点P(0,1),与x轴的正半轴交于A,B两点,且|AB|=2,则圆C的标准方程是( )
| A. | ${(x+\sqrt{2})^2}+{(y+1)^2}=2$ | B. | ${(x+1)^2}+{(y+\sqrt{2})^2}=2$ | C. | ${(x-\sqrt{2})^2}+{(y-1)^2}=2$ | D. | ${(x-1)^2}+{(y-\sqrt{2})^2}=2$ |
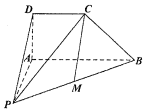 如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.
如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.