题目内容
在古希腊，毕达哥拉斯学派把1，3，6，10，15，…这些数叫做三角形数，因为这些数目的石子可以排成一个正三角形（如图）则第八个三角形数是 ．
考点：归纳推理
专题：推理和证明
分析：通过观察前几个图形中顶点的个数得，每一个图形中的顶点的个数都可以看成是一个等差数列的前几项的和，再利用等差数列的求和公式即可解决问题．
解答：
解：由已知中的前五个图形：
第一个三角形数为：1，
第二个三角形数为：1+2，
第三个三角形数为：1+2+3，
第四个三角形数为：1+2+3+4，
…
第n个三角形数为1+2+3+…+n=
n（n+1），
当n=8时，
n（n+1）=36，
故答案为：36
第一个三角形数为：1，
第二个三角形数为：1+2，
第三个三角形数为：1+2+3，
第四个三角形数为：1+2+3+4，
…
第n个三角形数为1+2+3+…+n=
| 1 |
| 2 |
当n=8时，
| 1 |
| 2 |
故答案为：36
点评：本题主要考查了归纳推理，以及数列递推式，属于基础题．所谓归纳推理，就是从个别性知识推出一般性结论的推理．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
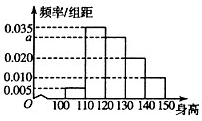从某小学随机抽取100名学生，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图），若要从身高在[120，130），[130，140），[140，150]三组内的学生中，用分层抽样的方法选取20人参加一项活动，则从身高在[120，130）内的学生中选取的人数应为下列哪个函数与y=x是相同函数（ ）
A、y=
| |||
B、y=
| |||
C、y=
| |||
| D、y=alogax（a＞0且a≠1） |
设a，b，c∈（-∞，0），则a+
，b+
，c+
（ ）
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| A、都不大于-4 |
| B、都不小于-4 |
| C、至少有一个不大于-4 |
| D、至少有一个不小于-4 |