题目内容
已知数列{an}的通项公式an=
,sn是它的前n项和,则s2014= .
| 1 |
| n(n+1) |
考点:数列的求和
专题:等差数列与等比数列
分析:先对其通项裂项,再代入前n项和Sn,通过各项相消即可求出Sn.
解答:
解:因为:an=
=
-
所以:s2014=(1-
)+(
-
)+(
-
)+…+(
-
)
=1-
=
.
故答案为:
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
所以:s2014=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2015 |
=1-
| 1 |
| 2015 |
=
| 2014 |
| 2015 |
故答案为:
| 2014 |
| 2015 |
点评:本题主要考查数列求和的裂项法,考查学生的运算能力.裂项法求和适用与数列的通项为分式形式,分子为常数,分母一般为某个等差数列相邻两项的乘积.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
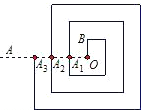 如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、
如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、