题目内容
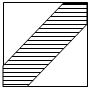在边长为25cm的正方形中挖去腰长为23cm的两个等腰直角三角形（如图），现有均匀的粒子散落在正方形中，问粒子落在中间带形区域的概率是考点：几何概型
专题：概率与统计
分析：求出带形区域的面积，并求出正方形面积用来表示全部基本事件，再由几何概型公式，即可求解．
解答：
解：因为均匀的粒子落在正方形内任何一点是等可能的
所以符合几何概型的条件．
设A=“粒子落在中间带形区域”则依题意得
正方形面积为：25×25=625
两个等腰直角三角形的面积为：2×
×23×23=529
带形区域的面积为：625-529=96
∴P（A）=
，
则粒子落在中间带形区域的概率是
．
故答案为：
．
所以符合几何概型的条件．
设A=“粒子落在中间带形区域”则依题意得
正方形面积为：25×25=625
两个等腰直角三角形的面积为：2×
| 1 |
| 2 |
带形区域的面积为：625-529=96
∴P（A）=
| 96 |
| 625 |
则粒子落在中间带形区域的概率是
| 96 |
| 625 |
故答案为：
| 96 |
| 625 |
点评：本题考查的知识点是几何概型的意义，简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
相关题目
以下是一组数据的茎叶图．现根据这个茎叶图画频率分布直方图，按[110，115），[115，120），…，[140，145）分为7组，则直方图中第3组小长方形的高为（ ）
| A、0.2 | B、0.4 |
| C、0.04 | D、0.08 |
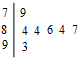如图是 a，b年在某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（ ）| A、83，1.5 |
| B、84，1.5 |
| C、85，1.6 |
| D、86，1.6 |
在面积为S的△ABC的边上AC任取一点P1，“使P1BC的面积大于
”的概率等于（ ）
| S |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设定义域为R的函数f（x），g（x）都有反函数，并且f（x-1）和g-1（2x-2）函数的图象关于直线y=x对称，若g（2）=2008，则f（1）的值为（ ）
| A、1005 | B、2008 |
| C、1003 | D、以上结果均不对 |
y=2cosx（
sinx+cosx）的一条对称轴为（ ）
| 3 |
A、x=
| ||
B、x=-
| ||
C、x=-
| ||
D、x=
|