题目内容
对于函数f(x)=eax-lnx(a是实常数),下列结论正确的一个是( )
A、a=1时,f(x)有极大值,且极大值点x0∈(
| ||
B、a=2时,f(x)有极小值,且极小值点x0∈(0,
| ||
C、a=
| ||
| D、a<0时,f(x)有极大值,且极大值点x0∈(-∞,0) |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:求出函数的导数,根据函数极值存在的条件,以及函数零点的判断条件,判断f′(x)=0根的区间即可得到结论.
解答:
解:∵f(x)=eax-lnx,
∴函数的定义域为(0,+∞),
函数的导数为f′(x)=aeax-
,
若a=
,f(x)=e
x-lnx,
则f′(x)=
e
x-
在(0,+∞)上单调递增,
f′(1)=
e
-1=
-1<0,f′(2)═
e-
=
(e-1)>0,
∴函数f(x)存在极小值,且f′(x)=0的根在区间(1,2)内,
故选:C
∴函数的定义域为(0,+∞),
函数的导数为f′(x)=aeax-
| 1 |
| x |
若a=
| 1 |
| 2 |
| 1 |
| 2 |
则f′(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
f′(1)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| e |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)存在极小值,且f′(x)=0的根在区间(1,2)内,
故选:C
点评:本题主要考查函数零点的判断以及函数极值的求解,利用函数和导数之间的关系是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,点M(1,2)为双曲线C右支上一点,且F2在以线段MF1为直径的圆的圆周上,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、2
| ||||||
C、3+2
| ||||||
D、
|
(文科)sin
π等于( )
| 2009 |
| 4 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
△ABC中,若
=
,则该三角形一定是( )
| a |
| cosB |
| b |
| cosA |
| A、等腰三角形但不是直角三角形 |
| B、直角三角形但不是等腰三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
正六棱锥P-ABCDEF中,G为PB的中点,则三棱锥D-GAC与三棱锥E-GAC的体积比
为( )
| VD-GAC |
| VE-GAC |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
将半径分别为2和1的两个球完全装入底面边长为4的正四棱柱容器中,则该容器的高至少为( )
| A、6 | ||
B、3+2
| ||
C、3+
| ||
D、3+
|
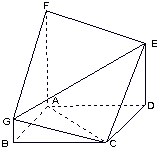 如图,多面体ABCDEFG中,FA⊥平面ABCD,FA∥BG∥DE,BG=
如图,多面体ABCDEFG中,FA⊥平面ABCD,FA∥BG∥DE,BG=