题目内容
以直线坐标系的原点为极点,x轴的非负半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l:y=x与圆C:ρ=4cosθ相交于A、B两点,则以AB为直径的圆的面积为 .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由圆C:ρ=4cosθ化为直角坐标方程(x-2)2+y2=4.可得圆心C(2,0),半径r=2.利用点到直线的距离公式可得:圆心C到直线y=x的距离d,利用弦长AB=2
,即可得出.
| r2-d2 |
解答:
解:由圆C:ρ=4cosθ化为ρ2=4ρcosθ,化为x2+y2=4x,
即(x-2)2+y2=4.圆心C(2,0),半径r=2.
∴圆心C到直线y=x的距离d=
=
.
∴弦长AB=2
=2
.
∴以AB为直径的圆的面积=π(
)2=2π.
故答案为:2π.
即(x-2)2+y2=4.圆心C(2,0),半径r=2.
∴圆心C到直线y=x的距离d=
| |2-0| | ||
|
| 2 |
∴弦长AB=2
| r2-d2 |
| 2 |
∴以AB为直径的圆的面积=π(
| 2 |
故答案为:2π.
点评:本题考查了极坐标方程化为直角坐标方程、点到直线的距离公式、圆的弦长公式,属于基础题.

练习册系列答案
相关题目
(文科)sin
π等于( )
| 2009 |
| 4 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
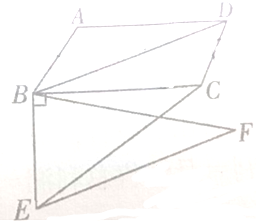 如图,在?ABCD中,AB=
如图,在?ABCD中,AB=