题目内容
已知|
|=
,|
|=1,且
与
的夹角为45°,则
•
= .
| a |
| 2 |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积的定义即可得出.
解答:
解:∵|
|=
,|
|=1,且
与
的夹角为45°,
∴
•
=|
| |
|cos45°=
×1×
=1.
故答案为:1.
| a |
| 2 |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| 2 |
| ||
| 2 |
故答案为:1.
点评:本题查克拉数量积的定义,属于基础题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,点M(1,2)为双曲线C右支上一点,且F2在以线段MF1为直径的圆的圆周上,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、2
| ||||||
C、3+2
| ||||||
D、
|
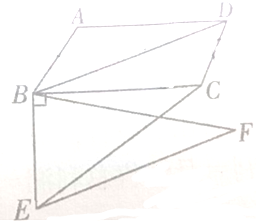 如图,在?ABCD中,AB=
如图,在?ABCD中,AB=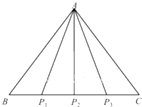 如图所示,△ABC是边长为1的正三角形,且点P在边BC上运动.当
如图所示,△ABC是边长为1的正三角形,且点P在边BC上运动.当