题目内容
若抛物线y=
x2上距点A（0，a）（a＞0）最近的点恰好是原点，求实数a的取值范围．
| 1 |
| 2 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先表示出距离，将抛物线代入化简，再研究其最值即可．
解答：
解：设距离为d，
根据题意得：d2=（y-a）2+x2 ，
∵y=
x2，
∴上式可整理得：d2=[y+（1-a）]2+2a-1，
∵a＞0且y≥0，
∴要求d的最小值，
则要考虑1-a的范围，
当1-a≥0时，y取0时d取最小值，
此时最近的点恰好是抛物线的顶点，刚好符合题意，
当1-a＜0，即a＞1时，y取a-1时有最小值，不成立．
∴a的范围为0＜a≤1．
根据题意得：d2=（y-a）2+x2 ，
∵y=
| 1 |
| 2 |
∴上式可整理得：d2=[y+（1-a）]2+2a-1，
∵a＞0且y≥0，
∴要求d的最小值，
则要考虑1-a的范围，
当1-a≥0时，y取0时d取最小值，
此时最近的点恰好是抛物线的顶点，刚好符合题意，
当1-a＜0，即a＞1时，y取a-1时有最小值，不成立．
∴a的范围为0＜a≤1．
点评：本题主要考查抛物线的几何性质，考查距离公式的运用，应注意分类讨论．
练习册系列答案
名校课堂系列答案
相关题目
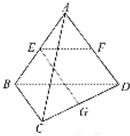如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：（1）
| EF |
| BA |
（2）
| EF |
| DC |
（3）EG的长；
（4）异面直线AG与CE所成角的余弦值．
设全集U=R，集合A={x|
≥0}，B={x|1＜2x＜8}，则（∁UA）∩B等于（ ）
| x+1 |
| x-2 |
| A、[-1，3） |
| B、（0，2] |
| C、（1，2] |
| D、（2，3） |