题目内容
已知函数f(x)为偶函数,若将f(x)的图象向右平移一个单位又得到一个奇函数,若f(2)=-1,则f(1)+f(2)+…+f(2013)等于( )
| A、-1 | B、0 |
| C、-1003 | D、1003 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的性质推导出函数的周期性,利用函数的周期性进行求解即可.
解答:
解:∵将f(x)的图象向右平移一个单位得到f(x-1),得到一个奇函数,
∴f(-x-1)=-f(x-1),
∵f(x)为偶函数,
∴f(-x-1)=-f(x-1)=f(x+1),
即f(x+2)=-f(x),
∴f(x+4)=f(x),即函数的周期是4.
∵f(2)=-1,
∴f(0)=f(2)=f(4)=-1,
当x=-1时,f(-1+2)=-f(-1),
即f(1)=-f(1),∴f(1)=0,
∵f(3)=-f(1)=0,
∴f(1)=0,f(2)=-1,f(3)=0,f(4)=-1,
∴f(1)+f(2)+f(3)+f(4)=0,
∴f(1)+f(2)+…+f(2013)=503×[f(1)+f(2)+f(3)+f(4)]+f(2013)=f(2013)=f(1)=0,
故选:B.
∴f(-x-1)=-f(x-1),
∵f(x)为偶函数,
∴f(-x-1)=-f(x-1)=f(x+1),
即f(x+2)=-f(x),
∴f(x+4)=f(x),即函数的周期是4.
∵f(2)=-1,
∴f(0)=f(2)=f(4)=-1,
当x=-1时,f(-1+2)=-f(-1),
即f(1)=-f(1),∴f(1)=0,
∵f(3)=-f(1)=0,
∴f(1)=0,f(2)=-1,f(3)=0,f(4)=-1,
∴f(1)+f(2)+f(3)+f(4)=0,
∴f(1)+f(2)+…+f(2013)=503×[f(1)+f(2)+f(3)+f(4)]+f(2013)=f(2013)=f(1)=0,
故选:B.
点评:本题主要函数值的计算,利用函数奇偶性的性质求出函数的周期性是解决本题关键,考查学生的推理能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
已知x,y满足
,则x+y的最小值为( )
|
| A、1 | B、2 | C、-1 | D、-2 |
直线x-y+3=0的倾斜角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)由下表定义:
若a1=2,an+1=f(an),n=l,2,3,…,则数列{an}的前2010项的和S2010=( )
| x | 1 | 2 | 3 | 4 | 5 |
| F(x) | 4 | 1 | 3 | 5 | 2 |
| A、6021 | B、6023 |
| C、6025 | D、6027 |
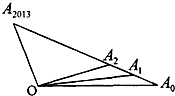 如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,
如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,| OA0 |
| a |
| OA2013 |
| b |
| a |
| b |
| OA0 |
| OA1 |
| OA2 |
| OA2013 |
A、1006(
| ||||
B、1007(
| ||||
C、2012(
| ||||
D、2014(
|