题目内容
15.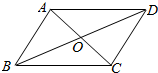 如图,已知0是?ABCD对角线的交点,给出下列结论:
如图,已知0是?ABCD对角线的交点,给出下列结论:①$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{BC}$,
②$\overrightarrow{AB}$+$\overrightarrow{CB}$=$\overrightarrow{AC}$,
③$\overrightarrow{AO}$$+\overrightarrow{OB}$=$\overrightarrow{AB}$;
④$\overrightarrow{CB}$$+\overrightarrow{CD}$=$\overrightarrow{CA}$,
⑤$\overrightarrow{AO}$$+\overrightarrow{CO}$=$\overrightarrow{DO}$$+\overrightarrow{BO}$,
其中正确的结论是③④⑤.(填序号)
分析 根据平行四边形法则与三角形法则对5个结论依次判断,从而解得.
解答 解:结合图象可知,
$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$≠$\overrightarrow{AB}$+$\overrightarrow{AC}$,故①错;
②$\overrightarrow{AB}$+$\overrightarrow{CB}$=$\overrightarrow{DC}$+$\overrightarrow{DA}$=$\overrightarrow{DB}$≠$\overrightarrow{AC}$,故②错;
由三角形法则,$\overrightarrow{AO}$$+\overrightarrow{OB}$=$\overrightarrow{AB}$,故③成立;
由平行四边形法则,$\overrightarrow{CB}$$+\overrightarrow{CD}$=$\overrightarrow{CA}$,故④成立;
$\overrightarrow{AO}$$+\overrightarrow{CO}$=$\overrightarrow{0}$,$\overrightarrow{DO}$$+\overrightarrow{BO}$=$\overrightarrow{0}$,故⑤成立;
故答案为:③④⑤.
点评 本题考查了平面向量线性运算的作法,属于基础题.

练习册系列答案
相关题目
5.设x、y、z是两两不等的实数,且满足下列等式:$\root{6}{{x^3{(y-x)}^3}}+\root{6}{{x^3{(z-x)}^3}}=\root{6}{y-x}-\root{6}{x-z}$,则代数式x3+y3+z3-3xyz的值是( )
| A. | 0 | B. | 1 | ||
| C. | 3 | D. | 条件不足,无法计算 |
6.若实数x,y满足$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=$\sqrt{{x}^{2}+{y}^{2}}$的最大值是( )
| A. | $\sqrt{43}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\sqrt{73}$ | D. | 3$\sqrt{2}$ |
3.若(x-1)100=a0x100+a1x99+…+a100对一切实数x恒成立,则a3+a97的值为( )
| A. | 0 | B. | C${\;}_{100}^{3}$ | C. | -2C${\;}_{100}^{3}$ | D. | 2100 |
20.过椭圆4x2+2y2=1的一个焦点F1的直线与椭圆相交于A、B两点,则A、B与椭圆的另一个焦点F2构成的△ABF2的周长等于( )
| A. | 2 | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |
7.设数列{an}满足:a1=1,a2=3,且2nan=(n-1)an-1+(n+1)an+1,则a20的值是( )
| A. | 4$\frac{1}{5}$ | B. | 4$\frac{2}{5}$ | C. | 4$\frac{3}{5}$ | D. | 4$\frac{4}{5}$ |
4.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=-x2+ax-1-a,若函数f(x)为R上的单调减函数,则a的取值范围是 ( )
| A. | a≥-1 | B. | -1≤a≤0 | C. | a≤0 | D. | a≤-1 |
12.设i是虚数单位,复数$\frac{4i}{1+i}$=( )
| A. | 2-2i | B. | -2-2i | C. | -2+2i | D. | 2+2i |