题目内容
20.过椭圆4x2+2y2=1的一个焦点F1的直线与椭圆相交于A、B两点,则A、B与椭圆的另一个焦点F2构成的△ABF2的周长等于( )| A. | 2 | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |
分析 把椭圆方程写成标准方程,求得椭圆的长轴长,再由椭圆定义求得答案.
解答  解:由椭圆4x2+2y2=1,得$\frac{{x}^{2}}{\frac{1}{4}}+\frac{{y}^{2}}{\frac{1}{2}}=1$,
解:由椭圆4x2+2y2=1,得$\frac{{x}^{2}}{\frac{1}{4}}+\frac{{y}^{2}}{\frac{1}{2}}=1$,
∴椭圆是长轴长为2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,焦点在y轴上的椭圆,
如图,
∴$|A{F}_{1}|+|A{F}_{2}|+|B{F}_{1}|+|B{F}_{2}|=4a=2\sqrt{2}$.
故选:D.
点评 本题考查椭圆的标准方程,考查了椭圆的简单性质,训练了利用椭圆定义求三角形的周长,是基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
5.在△ABC中,已知a=2,b=2$\sqrt{2}$,A=$\frac{π}{6}$,则∠B=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{4}$或$\frac{3}{4}$π | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
17.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递增区间为( )
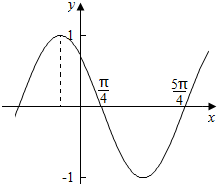

| A. | (kπ+$\frac{3}{4}$π,kπ+$\frac{7}{4}$π),k∈Z | B. | (kπ+$\frac{π}{4}$,kπ+$\frac{5π}{4}$),k∈Z | ||
| C. | (2kπ+$\frac{π}{4}$,2kπ+$\frac{5}{4}$π),k∈Z | D. | (2k+$\frac{3}{4}$π,2k+$\frac{7}{4}$π),k∈Z |
 A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.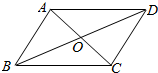 如图,已知0是?ABCD对角线的交点,给出下列结论:
如图,已知0是?ABCD对角线的交点,给出下列结论: