题目内容

5．设x、y、z是两两不等的实数，且满足下列等式：$\root{6}{{x^3{（y-x）}^3}}+\root{6}{{x^3{（z-x）}^3}}=\root{6}{y-x}-\root{6}{x-z}$，则代数式x3+y3+z3-3xyz的值是（　　）
A．0B．1
C．3D．条件不足，无法计算

分析 由x3（y-x）3≥0，x3（z-x）3≥0，y-x≥0，x-z≥0，可得：y=x=z=0，代入即可得出．

解答 解：由x3（y-x）3≥0，x3（z-x）3≥0，y-x≥0，x-z≥0，
可得：y=x=z=0，
∴代数式x3+y3+z3-3xyz=0，
故选：A．

点评 本题考查了函数的定义域、不等式的解法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
15．已知平面内A，B两点的坐标分别为（2，2），（0，-2），O为坐标原点，动点P满足|$\overrightarrow{BP}$|=1，则|$\overrightarrow{OA}+\overrightarrow{OP}$|的最小值是1．
16．设函数f（x）=$\sqrt{a{x^2}+bx+c}$（a，b，c∈R）的定义域和值域分别为A，B，若集合{（x，y）|x∈A，y∈B}对应的平面区域是正方形区域，则实数a，b，c满足（　　）
A．|a|=4B．a=-4且b2+16c＞0C．a＜0且b2+4ac≤0D．以上说法都不对
13．已知函数f（x）=x2+bx+1满足f（-x）=f（x+1），若存在实数t，使得对任意实数x∈[l，m]，都有f（x+t）≤x成立，则实数m的最大值为3．
20．先阅读参考材料，再解决此问题：
参考材料：求抛物线弧y=x2（0≤x≤2）与x轴及直线x=2围成的封闭图形的面积
解：把区间[0，2]进行n等分，得n-1个分点A（$\frac{2i}{n}$，0）（i=1，2，3，…，n-1），过分点Ai，作x轴的垂线，交抛物线于Bi，并如图构造n-1个矩形，先求出n-1个矩形的面积和Sn-1，再求$\underset{lim}{n→∞}$Sn-1，即是封闭图形的面积，又每个矩形的宽为$\frac{2}{n}$，第i个矩形的高为（$\frac{2i}{n}$）2，所以第i个矩形的面积为$\frac{2}{n}$•（$\frac{2i}{n}$）2；
Sn-1=$\frac{2}{n}$[$\frac{4•{1}^{2}}{{n}^{2}}$+$\frac{4•{2}^{2}}{{n}^{2}}$+$\frac{4•{3}^{2}}{{n}^{2}}$+…+$\frac{4•（n-1）^{2}}{{n}^{2}}$]=$\frac{8}{{n}^{3}}$[12+22+32+…+（n-1）2]=$\frac{8}{{n}^{3}}$•$\frac{n（n-1）（2n-1）}{6}$
所以封闭图形的面积为$\underset{lim}{n→∞}$$\frac{8}{{n}^{3}}$•$\frac{n（n-1）（2n-1）}{6}$=$\frac{8}{3}$
阅读以上材料，并解决此问题：已知对任意大于4的正整数n，不等式$\sqrt{1-\frac{{1}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{2}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{3}^{2}}{{n}^{2}}}$+…+$\sqrt{1-\frac{（n-1）^{2}}{{n}^{2}}}$＜an恒成立，则实数a的取值范围为[$\frac{π}{4}$，+∞）．
10．已知|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为120°，则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{13}$．
17．已知函数y=sin（x+$\frac{π}{6}$）+sin（x-$\frac{π}{6}$）+2cosx+a的最小值是1，则a的值为$1+\sqrt{7}$．
14．已知函数f（x）是（-∞，+∞）上的偶函数，若对于x≥0，都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=log2（x+1），求f（-2008）+f（2009）的值？
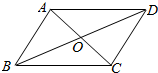15．如图，已知0是?ABCD对角线的交点，给出下列结论：
①$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{BC}$，
②$\overrightarrow{AB}$+$\overrightarrow{CB}$=$\overrightarrow{AC}$，
③$\overrightarrow{AO}$$+\overrightarrow{OB}$=$\overrightarrow{AB}$；
④$\overrightarrow{CB}$$+\overrightarrow{CD}$=$\overrightarrow{CA}$，
⑤$\overrightarrow{AO}$$+\overrightarrow{CO}$=$\overrightarrow{DO}$$+\overrightarrow{BO}$，
其中正确的结论是③④⑤．（填序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网