题目内容
3.若(x-1)100=a0x100+a1x99+…+a100对一切实数x恒成立,则a3+a97的值为( )| A. | 0 | B. | C${\;}_{100}^{3}$ | C. | -2C${\;}_{100}^{3}$ | D. | 2100 |
分析 根据二项式展开式定理,求出a3、a97的值,再计算a3+a97的值.
解答 解:∵(x-1)100=a0x100+a1x99+…+a100,
∴a3=-${C}_{100}^{3}$,
a97=-${C}_{100}^{97}$=-${C}_{100}^{3}$,
∴a3+a97=-2${C}_{100}^{3}$.
故选:C.
点评 本题考查了二项式定理的应用问题,是基础题目.

练习册系列答案
相关题目
18.在数列{an}中,a1=1,an+1•an=an-an+1
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=lg$\frac{{a}_{n+2}}{{a}_{n}}$,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=lg$\frac{{a}_{n+2}}{{a}_{n}}$,求数列{bn}的前n项和Sn.
13.已知$\overrightarrow{a}$、$\overrightarrow{b}$不平行,且$\overrightarrow{a}$•$\overrightarrow{b}$≠0,且$\overrightarrow{c}$=$\overrightarrow{a}$-($\frac{\overrightarrow{a}•\overrightarrow{a}}{\overrightarrow{a}•\overrightarrow{b}}$)$\overrightarrow{b}$,则向量$\overrightarrow{a}$与$\overrightarrow{c}$夹角为( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
 A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.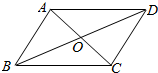 如图,已知0是?ABCD对角线的交点,给出下列结论:
如图,已知0是?ABCD对角线的交点,给出下列结论: