题目内容
4.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=-x2+ax-1-a,若函数f(x)为R上的单调减函数,则a的取值范围是 ( )| A. | a≥-1 | B. | -1≤a≤0 | C. | a≤0 | D. | a≤-1 |
分析 根据函数奇偶性的性质,结合函数单调性的关系进行求解即可.
解答 解:∵函数f(x)是奇函数,∴f(0)=0,
若函数f(x)为R上的单调减函数,
则满足当x>0时,函数为减函数,且当x=0时,-1-a≤0,
此时$\left\{\begin{array}{l}{-\frac{a}{-2}=\frac{a}{2}≤0}\\{-1-a≤0}\end{array}\right.$,即$\left\{\begin{array}{l}{a≤0}\\{a≥-1}\end{array}\right.$,
即-1≤a≤0,
故选:B
点评 本题主要考查函数单调性的应用,根据函数奇偶性和单调性的关系结合分段函数的单调性的性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.将函数f(x)=2sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{6}$,得到函数g(x)的图象,则g($\frac{π}{4}$)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
13.已知$\overrightarrow{a}$、$\overrightarrow{b}$不平行,且$\overrightarrow{a}$•$\overrightarrow{b}$≠0,且$\overrightarrow{c}$=$\overrightarrow{a}$-($\frac{\overrightarrow{a}•\overrightarrow{a}}{\overrightarrow{a}•\overrightarrow{b}}$)$\overrightarrow{b}$,则向量$\overrightarrow{a}$与$\overrightarrow{c}$夹角为( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
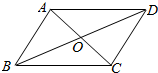 如图,已知0是?ABCD对角线的交点,给出下列结论:
如图,已知0是?ABCD对角线的交点,给出下列结论:
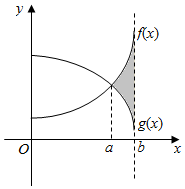 如图所示,已知${∫}_{0}^{b}$f(x)dx=11,${∫}_{0}^{b}$g(x)dx=9,${∫}_{0}^{a}$[g(x)-f(x)]dx=5.则图中阴影部分的面积为7.
如图所示,已知${∫}_{0}^{b}$f(x)dx=11,${∫}_{0}^{b}$g(x)dx=9,${∫}_{0}^{a}$[g(x)-f(x)]dx=5.则图中阴影部分的面积为7.