题目内容
10.计算5lg30•3lg2=15.(用数值作答)分析 根据指数幂的运算法则以及对数的运算法则进行化简即可.
解答 解:设5lg30•3lg2=x,
则:lgx=lg30lg5+lg2lg3=(1+lg3)(1-lg2)+lg2lg3=1+lg3-lg2=lg15,
解得x=15.
故答案为:15.
点评 本题考查对数运算法则的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.在数列{an}中,a1=1,an+1•an=an-an+1
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=lg$\frac{{a}_{n+2}}{{a}_{n}}$,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=lg$\frac{{a}_{n+2}}{{a}_{n}}$,求数列{bn}的前n项和Sn.
5.设数列{an}满足:a1=0,an+1=an+(n+1)3n.
(1)求数列{an}的通项公式;
(2)设bn=$\frac{4{a}_{n}+3}{{4}^{n}}$,求数列{bn}中的最大项的值.
(1)求数列{an}的通项公式;
(2)设bn=$\frac{4{a}_{n}+3}{{4}^{n}}$,求数列{bn}中的最大项的值.
19.将函数f(x)=2sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{6}$,得到函数g(x)的图象,则g($\frac{π}{4}$)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
 先阅读参考材料,再解决此问题:
先阅读参考材料,再解决此问题: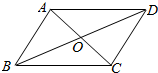 如图,已知0是?ABCD对角线的交点,给出下列结论:
如图,已知0是?ABCD对角线的交点,给出下列结论: