题目内容
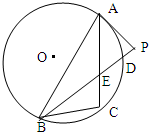 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.(1)求△ABP的面积;
(2)求弦AC的长.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(1)利用圆的切线的性质,结合切割线定理,求出PA,即可求△ABP的面积;
(2)由勾股定理得AE,由相交弦定理得EC,即可求弦AC的长.
(2)由勾股定理得AE,由相交弦定理得EC,即可求弦AC的长.
解答:
解:(1)因为PA是⊙O的切线,切点为A,
所以∠PAE=∠ABC=45°,…(1分)
又PA=PE,所以∠PEA=45°,∠APE=90°…(2分)
因为PD=1,DB=8,所以由切割线定理有PA2=PD•PB=9,
所以EP=PA=3,…(4分)
所以△ABP的面积为
BP•PA=
…(5分)
(2)在Rt△APE中,由勾股定理得AE=3
…(6分)
又ED=EP-PD=2,EB=DB-DE=8-2=6,
所以由相交弦定理得EC•EA=EB•ED=12 …(9分)
所以EC=
=2
,
故AC=5
…(10分)
所以∠PAE=∠ABC=45°,…(1分)
又PA=PE,所以∠PEA=45°,∠APE=90°…(2分)
因为PD=1,DB=8,所以由切割线定理有PA2=PD•PB=9,
所以EP=PA=3,…(4分)
所以△ABP的面积为
| 1 |
| 2 |
| 27 |
| 2 |
(2)在Rt△APE中,由勾股定理得AE=3
| 2 |
又ED=EP-PD=2,EB=DB-DE=8-2=6,
所以由相交弦定理得EC•EA=EB•ED=12 …(9分)
所以EC=
| 12 | ||
3
|
| 2 |
故AC=5
| 2 |
点评:本题考查圆的切线的性质、切割线定理、相交弦定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率是( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 一个四面体的三视图如图所示(图中三角形均为直角三角形),则该四面体的四个面中最大的面面积是
一个四面体的三视图如图所示(图中三角形均为直角三角形),则该四面体的四个面中最大的面面积是