题目内容
口袋中有大小、质地均相同的7个球,3个红球,4个黑球,现在从中任取3个球.
(1)求取出的球颜色相同的概率;
(2)若取出的红球数设为ξ,求随机变量ξ的分布列和数学期望.
(1)求取出的球颜色相同的概率;
(2)若取出的红球数设为ξ,求随机变量ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)设“取出的球颜色相同”为事件A,由此利用互斥事件概率计算公式能求出取出的球颜色相同的概率.(2)ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的分布列和数学期望.
解答:
解:(1)设“取出的球颜色相同”为事件A,
P(A)=
+
=
=
,
所以取出的球颜色相同的概率为
.…(4分)
(2)ξ的可能取值为0,1,2,3,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,…(8分)
ξ的分布列为:
…(10分)
∴Eξ=0×
+1×
+2×
+3×
=
=
.…(12分)
P(A)=
| ||
|
| ||
|
| 5 |
| 35 |
| 1 |
| 7 |
所以取出的球颜色相同的概率为
| 1 |
| 7 |
(2)ξ的可能取值为0,1,2,3,
P(ξ=0)=
| ||||
|
| 4 |
| 35 |
P(ξ=1)=
| ||||
|
| 18 |
| 35 |
P(ξ=2)=
| ||||
|
| 12 |
| 35 |
P(ξ=3)=
| ||||
|
| 1 |
| 35 |
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
∴Eξ=0×
| 4 |
| 35 |
| 18 |
| 35 |
| 12 |
| 35 |
| 1 |
| 35 |
| 45 |
| 35 |
| 9 |
| 7 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
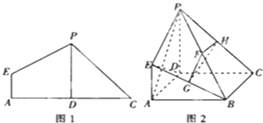 如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.