题目内容
12.已知函数f(x)=2cos2x-1,x∈R.(Ⅰ)求f($\frac{π}{6}$)的值;
(Ⅱ)求函数f(x)的最小正周期;
(Ⅲ)设g(x)=f($\frac{π}{4}$-x)+$\sqrt{3}$cos2x,求g(x)的值域.
分析 (Ⅰ)利用三角函数的恒等变换化简函数的解析式,从而求得f($\frac{π}{6}$)的值.
(Ⅱ)根据函数的解析式以及三角函数的周期性,求得函数f(x)的最小正周期.
(Ⅲ)化简g(x)的解析式,根据正弦函数的值域求得g(x)的值域.
解答 解:(Ⅰ)∵函数f(x)=2cos2x-1=cos2x,∴f($\frac{π}{6}$)=cos$\frac{π}{3}$=$\frac{1}{2}$.
(Ⅱ)函数f(x)=2cos2x-1=cos2x 的最小正周期为$\frac{2π}{2}$=π.
(Ⅲ)∵g(x)=f($\frac{π}{4}$-x)+$\sqrt{3}$cos2x=cos2($\frac{π}{4}$-x)+$\sqrt{3}$cos2x=sin2x+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
故g(x)的值域为[-2,2].
点评 本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦函数的值域,属于基础题.

练习册系列答案
相关题目
20.在空间中,下列命题正确的是( )
| A. | 若平面α内有无数条直线与直线l平行,则l∥α | |
| B. | 若平面α内有无数条直线与平面β平行,则α∥β | |
| C. | 若平面α内有无数条直线与直线l垂直,则l⊥α | |
| D. | 若平面α内有无数条直线与平面β垂直,则α⊥β |
7.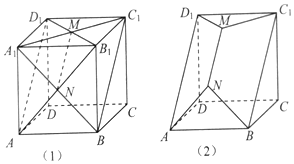 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{17}{24}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
 的顶点在原点,始边与x轴的非负半轴重合,终边落在直线
的顶点在原点,始边与x轴的非负半轴重合,终边落在直线 上,且
上,且 ,求
,求 的值.
的值. 的是
的是



 ,若
,若 ,则
,则 =___________。
=___________。