题目内容
某大学的8名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐4名同学(乘同一辆车的4名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自于同一年级的乘坐方式共有 种.
考点:计数原理的应用
专题:排列组合
分析:分类讨论,第一类,大一的孪生姐妹在甲车上;第二类,大一的孪生姐妹不在甲车上,再利用组合知识,问题得以解决.
解答:
解:由题意,第一类,大一的孪生姐妹在甲车上,甲车上剩下两个要来自不同的年级,从三个年级中选两个为
=3,然后分别从选择的年级中再选择一个学生为
=4,故有3×4=12种.
第二类,大一的孪生姐妹不在甲车上,则从剩下的3个年级中选择一个年级的两名同学在甲车上,为
=3,然后再从剩下的两个年级中分别选择一人为
=4,这时共有=3×4=12种
根据分类计数原理得,共有12+12=24种不同的乘车方式,
故答案为24.
| C | 2 3 |
| C | 1 2 |
| •C | 1 2 |
第二类,大一的孪生姐妹不在甲车上,则从剩下的3个年级中选择一个年级的两名同学在甲车上,为
| C | 1 3 |
| C | 1 2 |
| •C | 1 2 |
根据分类计数原理得,共有12+12=24种不同的乘车方式,
故答案为24.
点评:本题考查计数原理的应用,考查组合知识,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
函数y=-ln(x+1)的图象大致是( )
A、 |
B、 |
C、 |
D、 |
设A,B,C,D是平面直角坐标系中不同的四点,若
=λ
(λ∈R),
=μ
(μ∈R)且
+
=2,则称C,D是关于A,B的“好点对”.已知M,N是关于A,B的“好点对”,则下面说法正确的是( )
| AC |
| AB |
| AD |
| AB |
| 1 |
| λ |
| 1 |
| μ |
| A、M可能是线段AB的中点 |
| B、M,N可能同时在线段BA延长线上 |
| C、M,N可能同时在线段AB上 |
| D、M,N不可能同时在线段AB的延长线上 |
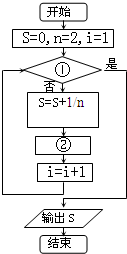
如图给出了计算
+
+
+…+
的值的程序框图,其中①②分别是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 60 |

| A、i<30,n=n+2 |
| B、i=30,n=n+2 |
| C、i>30,n=n+2 |
| D、i>30,n=n+1 |
