题目内容
已知集合{(x,y)|
}表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型,简单线性规划
专题:概率与统计
分析:作出不等式组对应的平面区域,求出对应的面积,结合几何概型的概率公式进行求解即可.
解答:
解:作出不等式组对应的平面区域如图,
则对应的区域为△AOB,
由
,解得
,即B(4,-4),
 由
由
,解得
,即A(
,
),
直线2x+y-4=0与x轴的交点坐标为(2,0),
则△OAB的面积S=
×2×
+
×2×4=
,
点P的坐标满足不等式x2+y2≤2区域面积S=
×π×(
)2=
,
则由几何概型的概率公式得点P的坐标满足不等式x2+y2≤2的概率为
=
,
故选:D
则对应的区域为△AOB,
由
|
|
 由
由
|
|
| 4 |
| 3 |
| 4 |
| 3 |
直线2x+y-4=0与x轴的交点坐标为(2,0),
则△OAB的面积S=
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
点P的坐标满足不等式x2+y2≤2区域面积S=
| 1 |
| 4 |
| 2 |
| π |
| 2 |
则由几何概型的概率公式得点P的坐标满足不等式x2+y2≤2的概率为
| ||
|
| 3π |
| 32 |
故选:D
点评:本题考查的知识点是几何概型,二元一次不等式(组)与平面区域,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据几何概型的概率公式进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知向量
,
满足:|
|=1,|
|=2,|
-
|=2则|
+
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
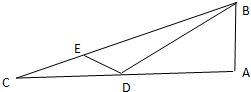 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=