题目内容
17.某程序框图如图所示,若输出S=$\frac{4}{3}$,则判断框中M为( )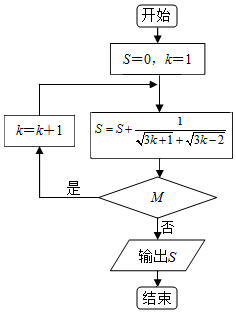
| A. | k<7? | B. | k≤6? | C. | k≤8? | D. | k<8? |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:第一次执行循环体,S=$\frac{1}{3}$,不满足结束循环的条件,故k=2;
第二次执行循环体,S=$\frac{\sqrt{7}-1}{3}$,不满足结束循环的条件,故k=3;
第三次执行循环体,S=$\frac{\sqrt{10}-1}{3}$,不满足结束循环的条件,故k=4;
第四次执行循环体,S=$\frac{\sqrt{13}-1}{3}$,不满足结束循环的条件,故k=5;
第五次执行循环体,S=1,不满足结束循环的条件,故k=6;
第六次执行循环体,S=$\frac{\sqrt{19}-1}{3}$,不满足结束循环的条件,故k=7;
第七次执行循环体,S=$\frac{\sqrt{22}-1}{3}$,不满足结束循环的条件,故k=8;
第八次执行循环体,S=$\frac{4}{3}$,满足结束循环的条件,
故退出的循环的条件,应为:k<8?,
故选:D
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.从5位男教师和3为女教师中选出3位教师,派往郊区3所学校支教,每校1人.要求这3位教师中男、女教师都要有,则不同的选派方案共有( )
| A. | 250种 | B. | 450种 | C. | 270种 | D. | 540种 |
5.已知函数$f(x)=\frac{1}{3}a{x^3}-\frac{1}{2}b{x^2}+x$,连续抛掷两颗骰子得到的点数分别是a,b,则函数f′(x)在x=1处取得最值的概率是( )
| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
12.已知函数f(x)=$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$,则不等式f(log2x)-f(log${\;}_{\frac{1}{2}}$x)≥$\frac{2({e}^{2}-1)}{{e}^{2}+1}$的解集为( )
| A. | [$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [$\frac{1}{2}$,2] |