题目内容
7.已知直角△ABC的一条直角边长是12$\sqrt{14}$,另外两条边长都是整数,那么,这样的直角三角形有4个,其中斜边长最大是505.分析 设另一条直角边为b,斜边为c,根据勾股定理和因式分解,得到c+b为偶数,c-b为偶数,所以144×14=72×28=56×36=1008×2,问题得以解决.
解答 解,设另一条直角边为b,斜边为c,
因为c2-b2=(c+b)(c-b)=144×14,且c-b<12$\sqrt{14}$<45,
设c+b=m,c-n=m,
则c=$\frac{m+n}{2}$,b=$\frac{m-n}{2}$,
又因为144×14为偶数,c,b都是整数,则c+b为偶数,c-b为偶数,
所以144×14=72×28=56×36=1008×2,
当$\left\{\begin{array}{l}{c+b=1008}\\{c-b=2}\end{array}\right.$,解得c=505,b=503,此时斜边最大,
故样的直角三角形有4个,斜边最大为505,
故答案为:4,505.
点评 本题考查了勾股定理和直角三角形的问题,关键是利用好两条边长都是整数,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
17.某程序框图如图所示,若输出S=$\frac{4}{3}$,则判断框中M为( )
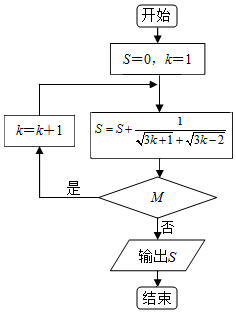

| A. | k<7? | B. | k≤6? | C. | k≤8? | D. | k<8? |
18.已知函数f(x)=$\left\{\begin{array}{l}{sin(2x+\frac{π}{3})(x≥0)}\\{cos(ωx+φ)(x<0)}\end{array}\right.$(其中ω>0,-$\frac{π}{2}$≤φ<$\frac{π}{2}$).若对于任意的x均有f(x-$\frac{π}{6}$)=f($\frac{π}{3}$-x),则sin(ωφ)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
14.为了研究数学、物理学习成绩的关联性,某位老师从一次考试中随机抽取30名学生,将数学、物理成绩进行统计,所得数据如表,其中数学成绩在120分以上(含120分)为优秀,物理成绩在80分以上(含80分)为优秀.
(1)根据表格完成下面2×2的列联表:
(2)若这一次考试物理成绩y关于数学成绩x的回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,
由图中数据计算成$\overline{x}$=120,$\overline{y}$=80,$\sum_{i=1}^{n}$(xi-$\overline{x}$)(yi-$\overline{y}$)=2736,$\sum_{i=1}^{n}$(xi-$\overline{x}$)2=8480,若y关于x的回归方程,据此估计,数学成绩每提高10分,物理成绩约提高多少分?(精确到0.1).
附1:独立性检验:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
附2:若(x1,y1),(x2,y2),…(xn,yn)为样本点,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$为回归直线,
则$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi |
| 1 | 108 | 82 | 11 | 124 | 80 | 21 | 122 | 64 |
| 2 | 112 | 76 | 12 | 136 | 86 | 22 | 136 | 82 |
| 3 | 130 | 78 | 13 | 127 | 83 | 23 | 114 | 84 |
| 4 | 132 | 91 | 14 | 80 | 73 | 24 | 121 | 80 |
| 5 | 108 | 68 | 15 | 138 | 81 | 25 | 88 | 52 |
| 6 | 140 | 88 | 16 | 141 | 91 | 26 | 142 | 83 |
| 7 | 143 | 92 | 17 | 109 | 85 | 27 | 125 | 69 |
| 8 | 99 | 72 | 18 | 100 | 80 | 28 | 135 | 90 |
| 9 | 106 | 84 | 19 | 92 | 73 | 29 | 112 | 82 |
| 10 | 120 | 77 | 20 | 132 | 82 | 30 | 128 | 92 |
| 数学成绩不优秀 | 数学成绩优秀 | 合计 | |
| 物理成绩不优秀 | |||
| 物理成绩优秀 | |||
| 合计 |
由图中数据计算成$\overline{x}$=120,$\overline{y}$=80,$\sum_{i=1}^{n}$(xi-$\overline{x}$)(yi-$\overline{y}$)=2736,$\sum_{i=1}^{n}$(xi-$\overline{x}$)2=8480,若y关于x的回归方程,据此估计,数学成绩每提高10分,物理成绩约提高多少分?(精确到0.1).
附1:独立性检验:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
则$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.