题目内容
12.已知函数f(x)=$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$,则不等式f(log2x)-f(log${\;}_{\frac{1}{2}}$x)≥$\frac{2({e}^{2}-1)}{{e}^{2}+1}$的解集为( )| A. | [$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [$\frac{1}{2}$,2] |
分析 先判断函数f(x)的奇偶性和单调性质,再原不等式转化为log2x≥1,解得即可.
解答 解:f(-x)=-$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$=-f(x),
∴f(log2x)-f(log${\;}_{\frac{1}{2}}$x)=f(log2x)-f(-log2x)=2f(log2x),
∵f(log2x)-f(log${\;}_{\frac{1}{2}}$x)≥$\frac{2({e}^{2}-1)}{{e}^{2}+1}$,
∴f(log2x)≥$\frac{{e}^{2}-1}{{e}^{2}+1}$=$\frac{e-{e}^{-1}}{e+{e}^{-1}}$=f(1),
∵f(x)=$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$=1-$\frac{2{e}^{-x}}{{e}^{x}+{e}^{-x}}$=1-$\frac{2}{{e}^{2x}+1}$为增函数,
∴log2x≥1=log22,
∴x≥2
故选:B.
点评 本题考查了奇偶性和单调性,以及对数函数的性质和不等式的解法,属于中档题.

练习册系列答案
相关题目
3.某程序框图如图所示,运行该程序,那么输出k的值是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
20.已知倾斜角为θ的直线,与直线x-3y+1=0垂直,则tanθ=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | $-\frac{1}{3}$ |
17.某程序框图如图所示,若输出S=$\frac{4}{3}$,则判断框中M为( )
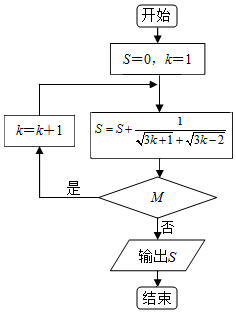

| A. | k<7? | B. | k≤6? | C. | k≤8? | D. | k<8? |
4.利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( )
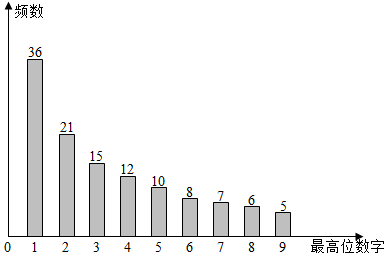

| A. | P=lg(1+$\frac{1}{d}$) | B. | P=$\frac{1}{d+2}$ | C. | P=$\frac{{(d-5)}^{2}}{120}$ | D. | P=$\frac{3}{5}$×$\frac{1}{{2}^{d}}$ |