题目内容

6．已知数列{an}满足an+1=2an，若a4+a6=3，则a7+a9的值是24．

分析 数列{an}满足an+1=2an，因此数列{an}是等比数列，则公比为q=2．再利用等比数列的性质求解即可．

解答 解：∵数列{an}满足an+1=2an，
∴数列{an}是等比数列，则公比为q=2．
∵a4+a6=3，
∴a7+a9=q3（a4+a6）=8×3=24，
故答案为：24．

点评 本题考查了等比数列的定义及其性质，考查了计算能力，属于基础题．

练习册系列答案
相关题目
16．已知实数x，y满足$\left\{\begin{array}{l}2x+y≥0\\ 4x-y≤8\\ x-y≥-1\end{array}\right.$，则x2+y2-2x的取值范围是[-1，19]．
17．某程序框图如图所示，若输出S=$\frac{4}{3}$，则判断框中M为（　　）
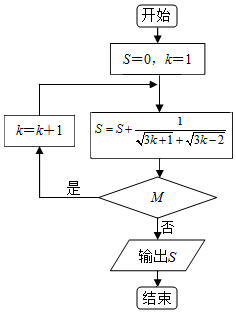
A．k＜7？B．k≤6？C．k≤8？D．k＜8？
14．设m，n是两条不同的直线，α，β是两个不同的平面，则下列叙述正确的是（　　）
A．若α∥β，m∥α，n∥β，则m∥nB．若α⊥β，m⊥α，n∥β，则m⊥n
C．若m∥α，n∥α，m∥β，n∥β，m⊥n，则α∥βD．若m⊥α，n?β，m⊥n，则α⊥β
1．设向量$\overrightarrow{a}$=（4cosα，sinα），$\overrightarrow{b}$=（sinβ，4cosβ），$\overrightarrow{c}$=（cosβ，-4sinβ）
（]）若$\overrightarrow{a}$与$\overrightarrow{b}$-2$\overrightarrow{c}$垂直，求tan（α+β）的值；
（2）求|$\overrightarrow{b}$+$\overrightarrow{c}$|的最大值；
（3）若tanαtanβ=16，求证：$\overrightarrow{a}$∥$\overrightarrow{b}$．
11．已知y=f（x）在点（1，f（1））处的切线方程为y=x-1，且f′（x）=lnx+1，则函数f（x）的最小值为-$\frac{1}{e}$．
18．已知函数f（x）=$\left\{\begin{array}{l}{sin（2x+\frac{π}{3}）（x≥0）}\\{cos（ωx+φ）（x＜0）}\end{array}\right.$（其中ω＞0，-$\frac{π}{2}$≤φ＜$\frac{π}{2}$）．若对于任意的x均有f（x-$\frac{π}{6}$）=f（$\frac{π}{3}$-x），则sin（ωφ）=（　　）
A．-$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{3}}{2}$C．$\frac{\sqrt{2}}{2}$D．$\frac{1}{2}$
15．若在△ABC中，|$\overrightarrow{AB}$|=3，|$\overrightarrow{BC}$|=5，|$\overrightarrow{AC}$|=4，则|5$\overrightarrow{AB}$+$\overrightarrow{BC}$|=$4\sqrt{10}$．
16．解方程：
1og4（3-x）+log${\;}_{\frac{1}{4}}$（3+x）=log4（1-x）+log${\;}_{\frac{1}{4}}$（2x+1）；（2）log${\;}_{\frac{2}{7}}$（8x-3x2）≤log${\;}_{\frac{2}{7}}$（2x2-5x）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网