题目内容
5.已知函数$f(x)=\frac{1}{3}a{x^3}-\frac{1}{2}b{x^2}+x$,连续抛掷两颗骰子得到的点数分别是a,b,则函数f′(x)在x=1处取得最值的概率是( )| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
分析 所有的(a,b)共计6×6=36个,函数f′(x)=ax2-bx在x=1处取得最值等价于f″(1)=2a-b=0,用列举法求得满足条件的(a,b)有3个,再根据概率公式计算即可
解答 解:连续抛掷两颗骰子得到的点数分别是a,b,共有36种等可能事件,
∵$f(x)=\frac{1}{3}a{x^3}-\frac{1}{2}b{x^2}+x$,
∴f′(x)=ax2-bx+1,
∵函数f′(x)=ax2-bx+1在x=1处取得最值,
∴f″(x)=2ax-b,
∴f″(1)=2a-b=0,
即2a=b,
满足的基本事件有(1,2),(2,4),(3,6),共3种,
故函数f′(x)在x=1处取得最值的概率为$\frac{3}{36}$=$\frac{1}{12}$,
故选:C.
点评 本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于中档题

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
15.设$z=\frac{1}{1+i}+i$(其中i为虚数单位),则$\overrightarrow{z}$的模等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
20.已知倾斜角为θ的直线,与直线x-3y+1=0垂直,则tanθ=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | $-\frac{1}{3}$ |
17.某程序框图如图所示,若输出S=$\frac{4}{3}$,则判断框中M为( )
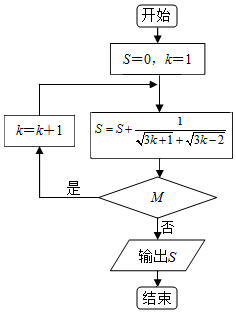

| A. | k<7? | B. | k≤6? | C. | k≤8? | D. | k<8? |
14.设m,n是两条不同的直线,α,β是两个不同的平面,则下列叙述正确的是( )
| A. | 若α∥β,m∥α,n∥β,则m∥n | B. | 若α⊥β,m⊥α,n∥β,则m⊥n | ||
| C. | 若m∥α,n∥α,m∥β,n∥β,m⊥n,则α∥β | D. | 若m⊥α,n?β,m⊥n,则α⊥β |
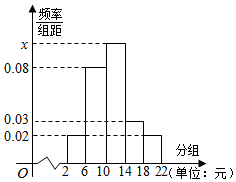 某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.
某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.