题目内容
7.已知二项式(1+xcosθ)5的展开式中第三项的系数与(x+5sinθ)3的展开式中第二项的系数相等,其中θ为锐角,则cosθ=$\frac{{\sqrt{3}}}{2}$.分析 二项式(1+xcosθ)5的展开式中第三项为T3=${∁}_{5}^{2}(xcosθ)^{2}$,可得系数为cos2θ${∁}_{5}^{2}$.(x+5sinθ)3的展开式中第二项为:${∁}_{3}^{1}{x}^{2}(5sinθ)^{1}$=5sinθ${∁}_{3}^{1}$x2,其系数为:15sinθ.利用系数相等即可得出.
解答 解:二项式(1+xcosθ)5的展开式中第三项为T3=${∁}_{5}^{2}(xcosθ)^{2}$=cos2θ${∁}_{5}^{2}$x2,其系数为cos2θ${∁}_{5}^{2}$,即10cos2θ.
(x+5sinθ)3的展开式中第二项为:${∁}_{3}^{1}{x}^{2}(5sinθ)^{1}$=5sinθ${∁}_{3}^{1}$x2,其系数为:15sinθ.
∴10cos2θ=15sinθ,化为2sin2θ+3sinθ-2=0,其中θ为锐角,
解得sinθ=$\frac{1}{2}$
则cosθ=$\sqrt{1-si{n}^{2}θ}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了二项式定理的应用、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.设$z=\frac{1}{1+i}+i$(其中i为虚数单位),则$\overrightarrow{z}$的模等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
12.某校高二(1)班一次阶段考试数学成绩的茎叶图和频率分布直方图可见部分如图,根据图中的信息,可确定被抽测的人数及分数在[90,100]内的人数分别为( )


| A. | 20,2 | B. | 24,4 | C. | 25,2 | D. | 25,4 |
17.某程序框图如图所示,若输出S=$\frac{4}{3}$,则判断框中M为( )
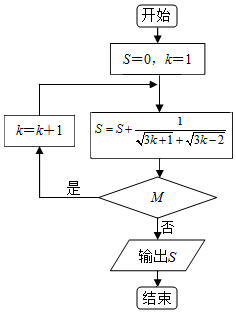

| A. | k<7? | B. | k≤6? | C. | k≤8? | D. | k<8? |