题目内容
8.从5位男教师和3为女教师中选出3位教师,派往郊区3所学校支教,每校1人.要求这3位教师中男、女教师都要有,则不同的选派方案共有( )| A. | 250种 | B. | 450种 | C. | 270种 | D. | 540种 |
分析 解答本题先理解题意中“这三位教师中男女教师都要有“,求解的方法有二,
法一:直接法:“这三位教师中男女教师都要有“,分为两类,有一位女教师,有二位女教师,由乘法原理求出即可;
法二:间接法:先求出7位教师中选出三位教师的选法种数,再求出只有女教师与只有男教师的选法种数,从总数中排除此两类选法即可得到所求的事件包含的种数.
解答 解:法一(直接法)::“这三位教师中男女教师都要有“,分为两类,有一位女教师,有二位女教师,
有一位女教师的选法种数为C52×C31=30,有二位女教师的选法种数为C51×C32=15,共有30+15=45种不同的选法,再分配到三个学校,
故有45A33=270种,
法二(间接法):从5名男教师和3名女教师中选出3位教师的不同选法有C83=56,
三位老师全是男教师的选法有C53=10种,三位教师全是女教师的选法有C33=1种
所以“这三位教师中男女教师都要有“,不同的选派方案有56-10-1=45种,
再分配到三个学校,
故有45A33=270种,
故选C.
点评 本题考查计数原理的运用,解答本题关键是熟练掌握分类原理与分步原理的定义,理解其适用范围,且能在具体的问题中可以灵活选用两个基本原理计数,本题解题用了两种方法,此是计数问题中常用的两个思路,题后应好好总结两个思路的特点.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.某程序框图如图所示,运行该程序,那么输出k的值是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
20.已知倾斜角为θ的直线,与直线x-3y+1=0垂直,则tanθ=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | $-\frac{1}{3}$ |
17.某程序框图如图所示,若输出S=$\frac{4}{3}$,则判断框中M为( )
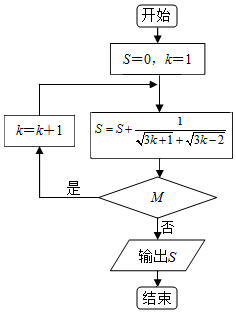

| A. | k<7? | B. | k≤6? | C. | k≤8? | D. | k<8? |
18.已知函数f(x)=$\left\{\begin{array}{l}{sin(2x+\frac{π}{3})(x≥0)}\\{cos(ωx+φ)(x<0)}\end{array}\right.$(其中ω>0,-$\frac{π}{2}$≤φ<$\frac{π}{2}$).若对于任意的x均有f(x-$\frac{π}{6}$)=f($\frac{π}{3}$-x),则sin(ωφ)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
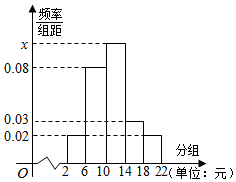 某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.
某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.