题目内容
17. 如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )
如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $3\sqrt{3}$ | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{3\sqrt{3}}}{4}$ |
分析 首先把三视图转化为立体图,然后根据三视图中的线段长和线面的关系,求出锥体的体积
解答  解:首先把几何体的三视图复原成立体图形
解:首先把几何体的三视图复原成立体图形
根据三视图中的线段长,得知:AD=$\frac{3}{2}$,CE=3,AC=2,
由于俯视图是边长为2的正三角形,进一步求得:AB=2,AF=1
所以BF=$\sqrt{3}$
根据三视图的特点得知:BF⊥底面DACE,
VB-DACE=$\frac{1}{3}$SDACE•BF=$\frac{1}{3}$×$\frac{1}{2}×(\frac{3}{2}+3)×2×\sqrt{3}$=$\frac{3\sqrt{3}}{2}$;
故选:A.
点评 本题考查的知识要点:三视图与立体图的相互转化,求立体图的体积,锥体的体积公式的应用,属于基础题型.

练习册系列答案
相关题目
2.若直线l1:x-2y+1=0与直线l2:x+ay-1=0平行,则l1与l2的距离为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
12.若函数$f(x)=4sinωx•{sin^2}({\frac{ωx}{2}+\frac{π}{4}})-2{sin^2}ωx(ω>0)$在$[{-\frac{π}{2},\frac{2π}{3}}]$上是增函数,则ω的取值范围是( )
| A. | (0,1] | B. | $({0,}\right.\left.{\frac{3}{4}}]$ | C. | [1,+∞) | D. | $[{\frac{3}{4}}\right.,+∞)$ |
2.如图是一个四面体的三视图,则该四面体的体积为( )


| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
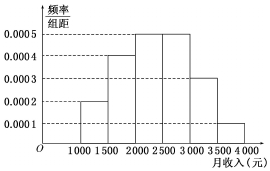 某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)). 如图,在三棱柱ABC-A1B1C1中,AB⊥BC,顶点A1在底面ABC内的射影恰好是AB的中点O,且AB=BC=2.OA1=2,
如图,在三棱柱ABC-A1B1C1中,AB⊥BC,顶点A1在底面ABC内的射影恰好是AB的中点O,且AB=BC=2.OA1=2,