题目内容
15.不超过实数x的最大整数称为x的整数部分,记作[x].已知f(x)=cos([x]-x),给出下列结论:①f(x)是偶函数;
②f(x)是周期函数,且最小值周期为π;
③f(x)的单调递减区间为[k,k+1)(k∈Z);
④f(x)的值域为[cos1,1).
其中正确的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 通过计算特殊值验证判断①,②;利用符合函数的单调性判断③,根据[x]-x的范围和余弦函数的性质判断④.
解答 解:对于①,∵f(π)=cos(3-π)=cos(π-3),f(-π)=cos(-4+π)=cos(4-π),
显然f(π)≠f(-π),∴f(x)不是偶函数,故①错误;
对于②,f(0)=cos(0-0)=cos0=1,而f(π)=cos(π-3)≠1,
∴f(0)≠f(π),即f(x)不是周期为π的函数,故②错误;
对于③,当x∈[k,k+1)时,[x]=k,
令t(x)=x-[x],则t(x)在区间[k,k+1)单调递增,且0≤t(x)<1,
又y=cosx在[0,1)上单调递减,
∴f(x)=cos([x]-x)=cos(x-[x])在[k,k+1)单调递减,故③正确;
对于④,∵-1<[x]-x≤0,∴f(x)取不到值cos1,且f(x)的最大值为1.
故④错误.
故选:B.
点评 本题考查命题的真假判断与应用,考查函数的图象,是中档题.

练习册系列答案
相关题目
18.将函数$y=4sin({4x+\frac{π}{6}})$的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移$\frac{π}{6}$个单位,则所得函数图象的一个对称中心为( )
| A. | (0,0) | B. | $({\frac{π}{3},0})$ | C. | $({\frac{π}{12},0})$ | D. | $({\frac{5}{8}π,0})$ |
3.设a>0,b>0,且a+b≤4,则有( )
| A. | $\frac{1}{ab}$≥$\frac{1}{2}$ | B. | $\frac{1}{a2+b2}$≤$\frac{1}{4}$ | C. | $\sqrt{ab}$≥2 | D. | $\frac{1}{a}$+$\frac{1}{b}$≥1 |
10.棱长为1的正方体截去一部分之后余下的几何体,其三视图如图所示,则余下几何体体积的最小值为( )
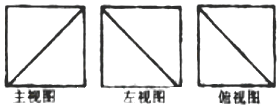

| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
20.某四面体的三视图如图所示,该四面体的体积为( )


| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
5.甲、乙两人对目标各射击一次,甲命中目标的概率为$\frac{2}{3}$,乙命中目标的概率为$\frac{4}{5}$,若命中目标的人数为X,则D(X)等于( )
| A. | $\frac{85}{225}$ | B. | $\frac{86}{225}$ | C. | $\frac{88}{225}$ | D. | $\frac{89}{225}$ |